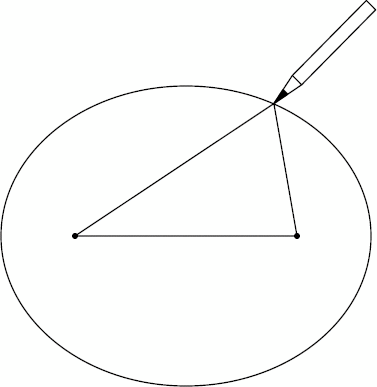
Figure 1. Drawing an ellipse with two nails, a board, and a loop of string.
This note started out in response to a thread in the Usenet group sci.astro.amateur asking why planetary orbits are elliptical. There are places you can go to get the mathematical derivation of those orbits, the poster observed, but nowhere you can get an ordinary explanation of just why the orbit is elliptical.
It turns out that the poster really wanted to know why the orbits weren't circular—he wasn't concerned about whether the particular out-of-round shape was an ellipse or something else—but consider the first question anyway. (I'm like that.) Can we say, succinctly and intuitively, how an elliptical orbit comes out from the so-called inverse square law?
My first reaction is to say no, and here's why. Scientists often prefer mathematical derivations to those in ordinary English, for two reasons: one, because they are more precise; and two, because they are more compact. It's possible, if you are very well versed in the language of mathematics, to turn a mathematical derivation into an ordinary English one that is just as precise, but the price for preserving that precision is an extraordinary lack of concision and intuitiveness.
As it turns out, even the mathematical derivation of the orbit is not a gem of brevity. Newton, in his Principia Mathematica, first derived the inverse square law of gravity from the properties of an elliptical orbit, and he needed a whole book of structure to build up underneath it. Even if we ignore the setup as merely preliminary, just the proof of the inverse square law itself fills up the better part of a page with extremely dense geometrical arguments that assume the reader is intimately familiar with the properties of ellipses. Today, even a physicist would be hard put to follow the arguments. To be fair, physicists today would use a different language to derive the orbital equations, but that derivation too is fairly lengthy.
Well, if the mathematical arguments are long, imagine what an ordinary English explanation would look like! So what are we doing here? I still think that a full explanation of why planetary orbits are elliptical is too involved to do in English; it's best to stick with the mathematics. But just perhaps, we can get enough of a flavor of the argument in ordinary English to satisfy our intuition. I warn you, however: This is still tricky going. The fact that it isn't simple and straightforward to demonstrate is an indication that Newton uncovered a relationship of great depth.
Just to be clear, here's what's really involved. Back in the early 17th century, Kepler announced that planetary orbits obeyed two simple laws. The first law states that planets move in elliptical orbits, with the Sun at one focus.
What does that mean, exactly—what is an ellipse? You can think of an ellipse as a squashed circle. You can draw one easily: Hammer two nails into a wooden board, near the center. Then, take a length of string long enough to wrap around the nails with room to spare, and tie it in a loop. Next, loop the string around the nails. If you stick a pencil inside the string loop and pull it taut, you can move the pencil around in a gently curving path. This path is an ellipse, and the two nails are at the ellipse's two foci (singular, focus). Figure 1 shows what this looks like.

Two foci? Yes, an ellipse has two of them. The Sun, for instance, is at one of the foci of the Earth's elliptical orbit. People often wonder what's at the other focus, expecting something unusual to be there—an anti-Earth, perhaps—but in fact, there is nothing at all of interest at the other focus. It is sometimes called the empty focus.
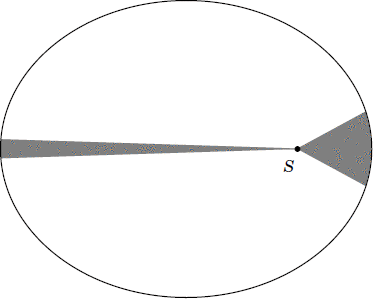
Kepler's second law states that in general, planets do not move in their orbits at a uniform speed. Rather, they move faster when closer to the Sun, and slower when further from the Sun. We can imagine them sweeping out little wedge-shaped slices of the orbital disc in each unit of time. The slices near the Sun are short and squat, while those far from the Sun are long and thin. Kepler's second law states that although the shapes are different, the areas are the same: Planets sweep out equal areas in equal times. Figure 2 illustrates this law.
What Newton showed was that given a planet that obeyed these two laws, the Sun must exert a force—that is, gravity—that drops off with increasing distance, in inverse proportion to the square of the distance (hence, "inverse square"). That is to say, if one planet is k times as far as another identical planet, the Sun's force is stronger on the second, closer one, by a factor of k squared.
Now that you know what I'm trying to show, let me reiterate that I'm not going to show it in any kind of rigorous detail. My emphasis will be on imparting a visceral intuition for why an orbit that adheres to Kepler's laws follows an inverse square law of gravity, without going too deeply into the mathematics.
To begin with, let's consider one interesting property of an ellipse. If you build a barrier in an elliptical shape, and you roll a tennis ball from one of the foci, in any direction whatsoever, it will bounce off the barrier and roll to the other focus.
This property applies to anything that bounces elastically, like a ball. For instance, if you put a light source at one focus of an ellipsoidal mirror, all the light will bounce off the mirror and converge at the other focus. (In fact, that's one reason why these points are called the foci.) An auditory analogue of this phenomenon can be found in some buildings, such as the U.S. Capitol Building, where you can whisper at one point and be heard at another point a long way away, even with people in the way. The reason is the ellipsoidal ceiling: the two points are the ceiling's foci.
In a geometrical sense, what this property represents is that if you draw a line perpendicular to the ellipse at any point P, the lines drawn from P make equal angles to that perpendicular. (OK, we have to use some mathematics.) This is shown in Figure 3.
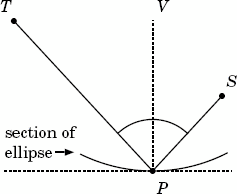
Now, suppose that P is a planet in an elliptical orbit, with its two foci at T and S. And suppose that this planet traces out a small section of its orbit in a certain period of time. If the Sun is at T, it sweeps out one wedge. But if the Sun is at S, it sweeps out a different wedge. (See Figure 4.)
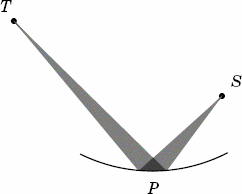
In moving along that small section of orbit, the planet changes its direction slightly. Since we're talking about the same stretch of orbit, it undergoes the same change in direction, whether the Sun is at T or it's at S. This change in direction can only come from the gravity of the Sun.
This sounds like we've just shown that the force of the Sun on a planet is the same for different distances, since TP is clearly longer than SP. But remember that the planet doesn't move at the same speed in the two different cases. If TP is twice as long as SP, as in Figure 4, then the shaded wedge extending from T contains twice the area of the shaded wedge extending from S; if it were three times as long, the larger wedge would have three times the area of the smaller wedge; and so on. Those ratios are only the same because of the equal-angle property we saw in Figure 3.
In short, if the Sun is at T, it takes twice as long to go along that section of orbit as it does if the Sun is at S.
This is critical! The distance covered is the same in either case, so the planet moves one-half as fast with the Sun at T as it does with the Sun at S. That means that the change in motion is only one-half as much, too. For instance, if you go through half of a circular orbit at 10 meters per second, the total change in motion is 20 meters per second, since you go from 10 meters per second in one direction to 10 meters per second in exactly the opposite direction. But if you do it at only 5 meters per second, the total change in motion is only 10 meters per second.
To be sure, the planet changes speed as well as direction, but it does so in proportion to the angle that TP or SP makes with the perpendicular, VP. Since both angles are the same, the proportions are the same, so the total change in motion is still only half as much with the Sun at T as it is with the Sun at S.
What's more, that change in motion also takes twice as long when the Sun is at T. If you combine those two effects—half the change in motion, in twice the amount of time—you can see that the rate of change in motion, the acceleration, is one-fourth as much if the Sun is at T as it is if the Sun is at S. And since the force exerted by the Sun must be proportional to the acceleration, it follows that the force is one-fourth, too.
Of course, there's only one Sun, and it can only be at one of the foci; it can't be continually moving back and forth between the foci. But the planet does move. And as Figure 5 shows, there is a spot in its orbit, labelled P', where the force exerted when the Sun is at S is the same as the force exerted when the Sun is at T and the planet is at P. So the planet at P' feels one-fourth the force from the Sun at S that the planet at P does.
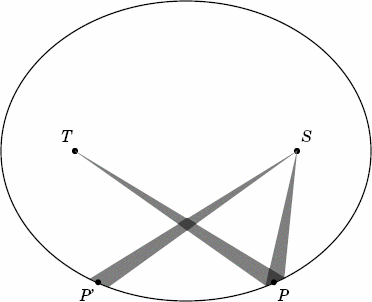
The fact that we ended up with a ratio of one-fourth comes from the fact that TP is twice as long as SP. If TP were some other factor k times as long as SP, the planet would undergo one kth the change in motion with the Sun at T, in k times as long a stretch of time, as it would with the Sun at S—meaning that the force would be smaller by a factor of k squared. So—aha!—here's our first glimpse of understanding the inverse square law of gravity.
We have to be careful, though, even when we're not quite being rigorous. We haven't shown that all points on the orbit are related by an inverse square law. We've only shown that that relationship exists between two symmetrically placed points P and P' on the orbit. We haven't said a thing about the relationship between any other kind of pairs of points. Nevertheless, it's an important first step, one that's worth setting apart and putting in bold:
Finding 1. An inverse square relationship exists between any two symmetrically placed points on the planet's orbit.
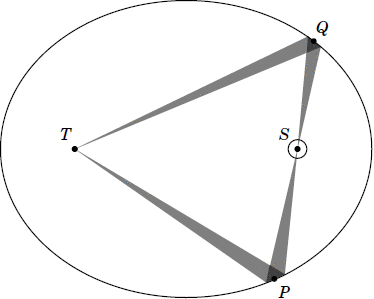
Next, let's try to relate another pair of points on the orbit. For this step, we'll fix the Sun at S. Suppose we extend the wedge from P, through the Sun at S, to a new point on the orbit, Q. These two wedges aren't the same size or shape, but they do have one thing in common: They make equal angles at S. I'll also draw lines connecting those wedges back to T. (See Figure 6.) Note that since P, S, and Q are all in a straight line, the wedges actually trace out a triangle, TPQ.
In this diagram, TP is still twice as long as SP. Notice that SP is longer than SQ—let's say, by a ratio of 4 to 3. (It could be any ratio, but picking a particular value will make the discussion easier.) That means that in some arbitrary units, TP has length 8, SP has length 4, SQ has length 3, and TQ has length 9; remember that because of the way an ellipse is constructed, TP+SP has to be equal to TQ+SQ. Figure 7, below, is just the same as Figure 6, but with all the lengths filled in. Pay close attention now; this is the toughest part of the entire explanation!
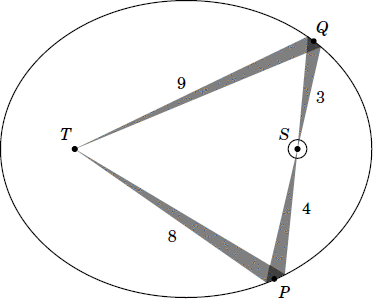
When the planet is at P, its distance from the Sun is 4, and when it's at Q, its distance is 3. To ensure that the planet sweeps out equal areas in equal times (Kepler's second law again), it must be moving faster at Q than at P, by a factor of 4 to 3. OK so far?
Now consider the thin wedges emanating in both directions from the Sun at S. They obviously cover the same angle. If we imagine the planet's orbit to be a kind of gigantic mirror, the section of mirror at Q is able to get that diverging wedge to converge again at T in a distance of 9, whereas the section at P is able to get it to converge at T in a distance of only 8. So the planet changes direction more at P than it does at Q, by a factor of 9 to 8.
Put those together, and you have the planet changing its motion more at Q than at P, by a factor of 4 x 8 = 32 to 3 x 9 = 27.
Except!
The "bounce" of the lines at P is shallower than it is at Q. This has two effects: First, it means that more of the Sun's gravitational effect is diverted into changing the planet's speed (as opposed to its direction) at P than it is at Q; and secondly, it means that the planet is moving faster at P than you might expect from Kepler's second law (because more of its motion is directed toward or away from the Sun and therefore has less impact on the area the planet sweeps). These two effects are weakest when the planet is at the ends of the elliptical orbit, and strongest when it's halfway in between. In fact, combined, they are proportional to the product of the planet's distance from the Sun, at S, and its distance from the empty focus, at T.
As a result, we have to apply corrections to the changes in motion at P and Q, equal to 4 x 8 = 32 and 3 x 9 = 27, respectively. That means that the actual, corrected changes of motion at P and at Q are related by a factor of 32 x 27 to 27 x 32; or, in other words, they're exactly equal!
But remember that the planets don't take equal times to sweep out the wedges at P and Q. It takes longer to sweep out the wedge at P, because that wedge covers more area, by a ratio of 4 to 3, squared, or 16 to 9. Since the change in motion is the same, the rate of change in motion—the acceleration, again—must be greater at Q by that same 16 to 9 ratio. Of course, that's just what the inverse square law says.
There's nothing in what I wrote that depends specifically on the particular lengths I chose, so the same reasoning can be applied to any two opposite points on the orbit:
Finding 2. An inverse square relationship exists between any two points on the planet's orbit that are opposite the Sun from one another.
At last, we're ready to put everything together. What we're going to show is that any point on the orbit is related by an inverse square law to a special point, called the perihelion point. That point is the one that's closest to the Sun ("perihelion" comes from two Greek words meaning "around" and "Sun"), and it lies on one "end" of the ellipse.
Here's how we're going to do it. We start out at a point P on the orbit. We draw a line from P through S to a point Q; Finding 2 tells us that P and Q are related by the inverse square law.
Then, we move from Q across to a symmetrically placed point Q'; here, it is Finding 1 that tells us that the inverse square law relates Q' to Q, and therefore back to P. Then we draw a line from Q' through S to R, then across to R', etc. We keep applying Findings 1 and 2 alternately to give us a whole slew of points, all related by the inverse square law. Figure 8 illustrates the basic idea.
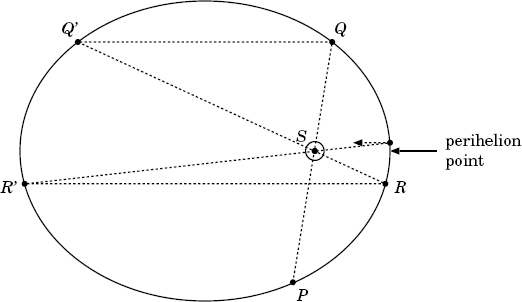
As we collect more and more points under the unbrella of the inverse square law, we get closer and closer to the perihelion point. In fact, the limit of this sequence is always the perihelion point. (Actually, there are two limits; the other limit is the aphelion point, the point furthest from the Sun, and directly opposite the perihelion point. Either one will serve our purposes.) Since any arbitrary point on the orbit can be related to the perihelion point by the inverse square law, all points on the orbit are so related:
Finding 3. An inverse square relationship exists amongst all the points on the planet's orbit.
And that's what we wanted to see all along.
Of course, Newton went on to show much more than just this. Using his methods, he was able to use another law of Kepler to show that the inverse square law applied equally to all the planets, to apply this universal law to determine the perturbative effects of one planet upon another, to explain the precession of the equinoxes, etc.—all of which are beyond the scope of this article. But for those who might have been mystified by the appearance of the inverse square relationship out of the ellipse, I hope this article has given you at least an inkling of it.
Copyright (c) 2006, 2010 Brian Tung