Somebody asked:
Suppose a planet travels in an elliptical orbit around the Sun, according to Kepler's laws. What is the expected position of the planet, averaged over time?
Suppose, without loss of generality, that the ellipse has its major axis along the x-axis, with the center at the origin. The question then asks us to derive X, the time-averaged x-position of the planet. We don't need to figure out the time-averaged y-position, since by symmetry arguments, it must be zero on average.
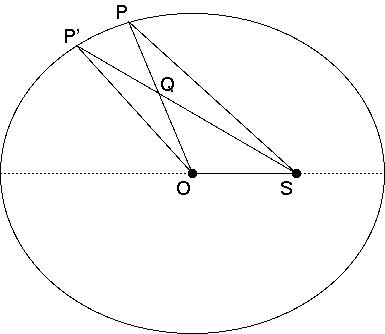
In order to compute the compute X, we must weight each x-position by the time spent at that position, taken to the limit as each time slice goes to zero. By Kepler's second law, we may equivalently weight by the area of a wedge, extending from the Sun to the planet's path. Let's put that in coordinate terms. Consider an elliptical orbit, centered at the origin at O(0, 0), with semi-major axis equal to 1. That is, the ends of the orbit are at (–1, 0) and (1, 0). The Sun is, let's say, at one focus of the ellipse, at S(e, 0), where e is the eccentricity of the ellipse.
Suppose that the planet is currently at P(x, y). Over an infinitesimal period of time, it will move to a point P'(x', y'). Then the position coordinate x is to be weighted by the area of a wedge, extending from S, sweeping from P to P'. Let's call this wedge W1.
The key to the enterprise is recognizing that the area of W1 is almost equal to the area of another wedge, W2, which is the wedge, extending from the origin O, and sweeping from P to P'. In particular, we may write that
area(W1) = area(W2) + small amount
We'll get to that small amount in a moment. Remember, again, that X is equal to
the average x-position, weighted by area(W1)
By the above relation, X is also equal to
the average x-position, weighted by area(W2), plus
the average x-position, weighted by that small amount
Note that for every wedge W2 going to a P with a positive x-position, there is a corresponding wedge W2– going to a P– with the corresponding negative x-position. Therefore, the first quantity in the equation above for X is zero! That is, X is simply equal to
the average x-position, weighted by that small amount
Now, what is that small amount? As we stated above, it is the area of W1 minus the area of W2. By consulting the diagram below,

we see that this is equal to
area(SPP') – area(OPP') = area(SQP) – area(OQP') = area(SOP) – area(OSP') = ey/2 – ey'/2 = e(y–y')/2
This is the "small amount" by which we must weight all the x-positions. We do this simply by multiplying them together, to yield xe(y–y')/2, which we'll rewrite as (e/2)x(y–y'). This quantity must be summed as the planet P traverses the entire ellipse. Since the value of e/2 does not change, we'll just sum x(y–y') over the entire ellipse, and multiply e/2 in at the end.
As the planet moves from P to P', the quantity x(y–y') can naturally be interpreted as an area—the area of a rectangle whose width extends from the y-axis to the planet's position, and whose height is the height difference between P and P', as shown in the diagram below. Now, when x is positive, the height difference y–y' is negative, and when x is negative, the difference y–y' is positive. Therefore, to be precise, we must interpret these areas as negative areas.
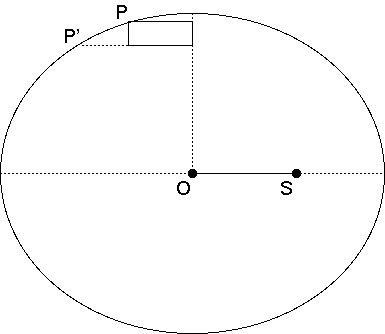
Now observe! As the planet moves around the entire ellipse, these small rectangles combine to cover the entire ellipse, without overlap, and in the limit, without error either. The sum of x(y–y'), over the entire ellipse, is simply the area of the ellipse. We must be sure to interpret it as the negative area—that is, –A (where A is the geometrical area of the ellipse). And if the sum of x(y–y') over the circle is –A, then the sum of (e/2)x(y–y') is –(e/2)A.
All that remains now, is to divide that result by the area of the ellipse which we averaged the x-position over. That area is, again, A, so that the average x-position, weighted by the wedge area W1, or by time (either is equivalent to the other) is just
–(e/2)A / A = –e/2
And this is just the position halfway between the empty focus, and the center of the ellipse. Q.E.D.
Copyright (c) 2001 Brian Tung