Figure 1.
In this little exposition, I'm going to explain coma and other geometric aberrations from first principles and elementary geometry.
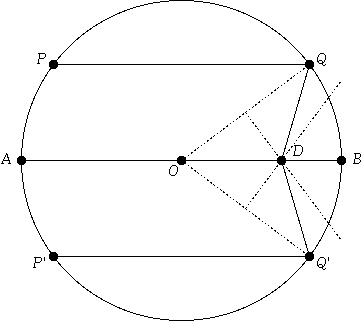
Suppose we have a spherical mirror, whose cross section we represent by the unit circle centered at the origin O. Consider three incoming rays of light; we will represent these rays by the following three chords:
AB, which passes horizontally through the origin;
PQ, which passes horizontally, but above AB; and
P'Q', which passes horizontally and an equal amount below AB.
These three rays, after reflecting off the right semicircle, intersect the line AB at a point D, which can be constructed straightforwardly. Simply draw the perpendicular bisectors of OQ and OQ'. These will both intersect AB at D. The following diagram should make this clear:

From this diagram, we can see that by constructing point D where the perpendicular bisector of (for example) OQ intersects AB, we have constructed an isosceles triangle, OQD. From this, it follows that angle OQD is congruent to angle QOD. It is also evident that angle QOD is congruent to angle OQP. Thus, angle OQD is congruent to angle OQP, and the law of reflection is satisfied. A similar argument applies for the reflection of the ray of light at P'Q'.
Next, let's consider what happens to these three rays if they are still parallel, still strike the right semicircle at Q, B, and Q', but are no longer horizontal. Let's call these three new rays, RQ, CB, and R'Q'. We shall see that the reflections of these three new rays no longer intersect at one point. If we follow the reflection of R'Q', we see in Figure 2 that it intersects the reflection of RQ at E, then intersects the reflection of CB at V.
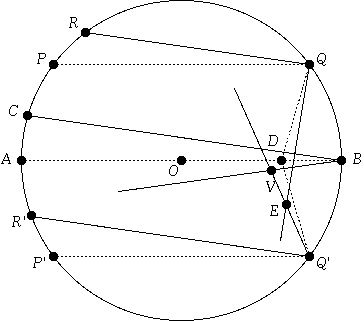
Suppose we try to determine the size of angle QEQ'. We see that it is larger than angle QDQ' by an amount equal to angle DQE minus angle DQ'E. But angle DQE is congruent to angle RQP, and angle DQ'E is congruent to angle R'Q'P'. Since the incoming rays are still parallel, these angles must all be equal, so that angle QDQ' is congruent to angle QEQ'.
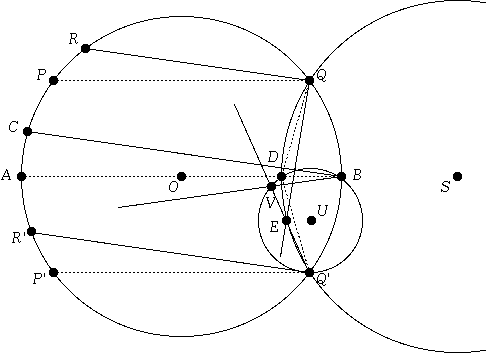
But the locus of all points E such that angle QEQ' is congruent to angle QDQ' is simply the unique circle containing the points Q, D, and Q'! In other words, no matter the angle CBA—that is, no matter how far off axis the object and image are—the intersection of the rays at RQ and R'Q' must land somewhere on this circle. Let the center of this circle be called S. (Note that if angle QOQ' is equal to 90 degrees, then Q, D, and Q' all lie on a straight line, so that S is at infinity, and if angle QOQ' is greater than 90 degrees, then S is actually to the left of D.) Similar reasoning shows us that angle BVQ' is congruent to angle BDQ', so the locus of all points V is simply the unique circle U containing the three points B, D, and Q'. This is all shown in Figure 3.
Now, let's consider what happens if we return to the horizontal rays, but move PQ and P'Q' steadily closer toward the diameter AB. In that case, the point D steadily moves toward the point F, halfway between O and B, which is the nominal focal point of the mirror. In fact, from the above discussion, D is precisely as far from O as is the point T, which is the the point on OQ directly above F. (See Figure 4.)
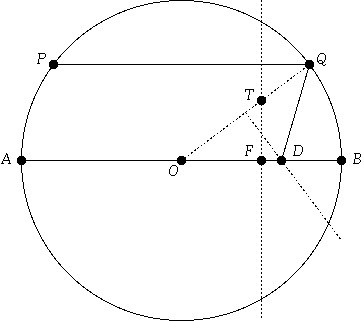
In the limit, as PQ and P'Q' both move toward AB, the circles S and U converge to the circle G, which has radius 1/4, and intersects AB at F and B. (See Figure 5.)
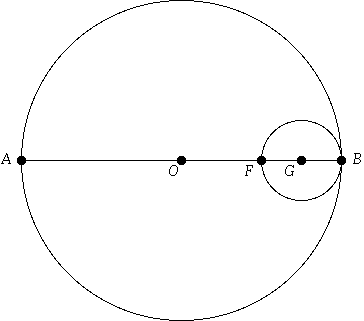
We can now characterize various aberrations in terms of these geometrical figures. The movement of D toward F as Q and Q' approach each other, and toward B as they separate, is spherical aberration. The curvature of circle G is the field curvature. And the amount by which E is under the reflection line BV is what we call coma (tangential coma, to be more specific). Note that coma varies with both off-axis angle (the angle CBA) and the aperture (the separation of Q and Q'). Finally, note that in Figure 3, D is to the left of E; the horizontal distance between them (ignoring the vertical separation) is the astigmatism.
An interesting observation from this derivation is that a spherical mirror has both coma and, of course, spherical aberration. A paraboloidal mirror would have D coincident with F no matter how far apart Q and Q' were, so it does not possess spherical aberration. However, since the circles S and U still exist, it does have coma, and since they both converge to G as Q and Q' approach each other, it has field curvature as well.
Copyright (c) 2002 Brian Tung