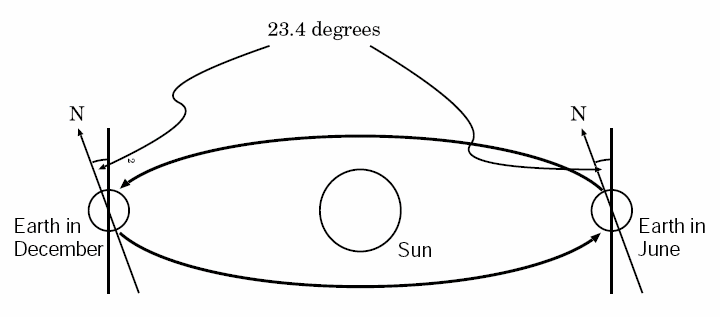
Figure 1. Axial tilt with respect to the orbital plane.
Look, Ma! Top of the world!
—Jimmy Cagney, in White Heat
ONE OFTEN derides inventions by observing, "Nothing new under the sun." (The phrase is used in the Bible to express the futility of all work.) Which seems all too easy to me. Of course almost all inventions rely largely (perhaps predominantly) on existing technology, either directly or by inspiration. That doesn't mean that the invention isn't innovative.
But there is another interpretation of that saying, which is that people understand most new things by way of analogy—an idea put forth by, among others, Douglas Hofstadter in his book, Metamagical Themas (Basic Books, 1987). Hofstadter argues persuasively that the human brain apprehends new concepts by trying to fit them into a template followed by older concepts, a fit that is often imperfect. Nonetheless, this may well explain the application of precedence in law, and the development of metaphor in language.
Analogies are imperfect, though. Richard Feynman, the great Caltech physicist, explained that there are times that you can't resort to analogy because any understanding based on them will be flawed. You could explain how magnets work by analogy to rubber bands. But rubber bands don't have polarity, as magnets do, and what's more, rubber bands work because of electromagnetic forces between the atoms making them up, so the explanation is circular, anyway.
As you've probably guessed, I have an example in astronomy, too, and as you can probably also guess, I'll get to it…in time.
A common misconception is that the word "astronomy" comes from Greek words meaning "the naming of stars." Usually, this derivation is followed by the supposition that the word "astrology" comes from Greek words meaning "the study of stars," thus indicating that it is astrology and not astronomy that is the legitimate sphere of scientific work.
The short and sweet answer to that claim is that etymology is a poor guide to meaning. (One of my favorite examples of this is the word "nice," which comes from Latin nescius, meaning ignorant.) But even if we do look at etymology, the "-logy" in "astrology" didn't mean originally mean "study"; that was a later derived meaning. The original meaning came from Greek logos, meaning "word." So etymologically speaking, astrology is about what the stars tell us—just about what it means today.
Then, too, the "-nomy" in "astronomy" doesn't mean "name," either. Rather, it comes from Greek nemein, "to arrange." Astronomy is then about the arrangement of the stars. If we think of an astronomer as someone who deduces the laws that govern how stars are arranged in space and time, that's not far off, either.
But early astronomers were involved in the arrangement of stars in a more direct way, too. They may not have deduced any laws of nature, but they did record the way the stars were arranged in the sky.
Before we go on, let me explain a bit about how the sky seems to work from our perspective. Like the Sun, the stars generally appear to rise in the east and set in the west. This apparent motion is not intrinsic to the stars themselves, but is an optical illusion caused by the Earth's rotation.
If one carefully watches the stars throughout the course of a night, or several successive nights, one notices that the stars may move across the sky, but they are stationary with respect to one another. That is to say, the stars appear to revolve around the Earth in a single piece. So even though one can't say of a given star where it will be in the sky—high in the east, or low in the south, or whatever—we can say where it's located in relation to its celestial neighbors.
Moreover, any given star will follow the same path night after night. If Sirius, the brightest star in the night sky, passes just over a mountaintop as seen on a certain night, from a certain vantage point, it will pass just over that mountaintop on each succeeding night, as seen from that same vantage point. The timing might change—it might happen at dawn in the fall and at dusk in the spring—but the path followed by Sirius is the same. This makes it possible to assign numerical coordinates to each star, just as we assign longitude and latitude to points on the Earth.
One of the earliest to do all this was a Greek named Timocharis, who lived around 300 B.C. Not much is known about him. We do know that he created a star catalogue, which recorded the names and locations of perhaps a few hundred stars, and we only know that because later Greek astronomers mention him in their writings. No copy of Timocharis's catalogue itself has survived.
Perhaps a century and a half later, a new star catalogue was created by a better known Greek astronomer, Hipparchus of Nicaea (190–120 B.C.). According to the Greek historian, Pliny the Elder, Hipparchus put together his catalogue because he had observed a new star. Or, at the least, he suspected he had. He had no way to be sure. Once the star appeared, Hipparchus had no photographs, no sketches, no record to consult to figure out what the sky looked like beforehand. There was Timocharis's catalogue, but it was not complete enough to verify that what Hipparchus thought was a new star was indeed new. It might be that Timocharis had just decided not to record it.
So Hipparchus created his own catalogue, one that was complete enough that later astronomers would be able to identify any new stars. To do this, he needed to make sure that he recorded the brightnesses, or magnitudes, of the stars, and that the catalogue included just all the stars brighter than a certain magnitude. Otherwise, an astronomer would have no way to decide whether a star didn't appear in the catalogue because it really was new, or simply because Hipparchus hadn't seen fit to include it. If a star was bright enough to be included in Hipparchus's catalogue, but was not, it had to be new.
No copies of this catalogue has survived today in its original form, either, but the last great astronomer of Greek times, Ptolemy (85–165), used it and augmented it to form the stellar catalogue of his monumental astronomical work, the Almagest.
As far as we know, Hipparchus never again observed a new star in the sky, but he did make an interesting and very important discovery. After completing his catalogue, he compared it with that of Timocharis. (Although Timocharis's catalogue was incomplete, it had enough stars in common with Hipparchus's catalogue to make a comparison worthwhile.) Hipparchus found that his coordinates were a little off from the ones that Timocharis had recorded. The difference was not much—maybe one or two degrees, the width of your thumb when held up at arm's length—but it was noticeable.
This in itself is not so astonishing. If you ask two people with a compass what the bearing of a distant landmark is, you would expect them to come up with slightly different answers. It would not be surprising at all for one to say it was, for instance, 14 degrees east of north, and for the other to say it was 16 degrees east of north. It just isn't that easy to determine an angle to better than a degree or so with the unaided eye, and of course neither Hipparchus nor Timocharis had access to anything like a telescope.
However, Hipparchus found that the coordinates were all off in the same direction, something that would be difficult to attribute to random variation or error. It was as though Hipparchus and Timocharis had observed the same sky, but Hipparchus's sky had been turned an extra degree or two, in a way that had nothing to do with daily rising and setting. Hipparchus imagined the stars to be affixed to a giant, transparent sphere, called the celestial sphere, that turned around the Earth once a day, which accounted for the daily motion of the stars.
In order to account for the extra motion he had found, he imagined that celestial sphere to be attached, in turn, to an external sphere that turned extremely slowly—so slowly, in fact, that it had only rotated degree or two in the century and a half between Timocharis's catalogue and Hipparchus's.
Hipparchus tried to calculate how long it would take for this outer sphere to make a complete rotation. (That it would make a complete rotation seems like a logical leap to us, but to Hipparchus, steeped in the Greek tradition of venerating circular motion, it wasn't.) The task was tricky, given the inherent inaccuracies in assembling a stellar catalogue from observations made by the unaided eye, but Hipparchus managed. He concluded that the sphere turned at a rate of one degree every century—or equivalently, that it made a complete rotation of 360 degrees in 360 centuries, or 36,000 years.
Hipparchus even gave this extra motion a name: the precession of the equinoxes. He called it that because as a result of the rotation of this extra sphere, the points at which the Earth's equatorial plane cut its orbital plane came earlier and earlier each year; in other words, each spring equinox preceded the previous spring equinox, and each autumn equinox preceded the previous autumn equinox—albeit by a vanishingly small amount.
He had no idea what caused it, though. And when Ptolemy and then medieval astronomers built upon the work of Hipparchus in their own astronomical treatises, they had no idea what caused precession, either. To be fair, they were more interested in accurately capturing celestial motions than they were in explaining them.
A better understanding of why precession occurs would have to wait until the development, in the late 17th century, of a quantitative theory of gravitation by the great English scholar, Isaac Newton (1642–1727), which I described at some length in "The Grand Illusion." Newton deduced that every pair of particles in the universe attract one another with a force that increases with the masses of the particles and decreases as the square of the distance between them. (This latter property is why Newton's law of universal gravitation is called an inverse-square law.)
This would seem to be a computational thorn in the side of physicists, since even objects like the Earth and the Moon that are puny on an astronomical scale contain trillions of trillions of particles, each of which attracts every other particle in the universe.
Fortunately, Newton provided the analytical tools necessary to treat the Earth and Moon and other celestial bodies as single, very massive particles, provided they satisfied a number of properties. One was that they must be spherical. Another was that their density must vary in the same way in each direction from their center. In other words, the Earth need not be uniformly dense throughout, but if it has a certain density 500 km beneath the surface in one spot, it must have that same density 500 km beneath the surface everywhere else.
It turns out that Newton's law of gravity can be applied to the Earth, the Moon, the Sun, and the other planets as individual particles, and it yields fruitful results without undue hardship—an indication that the Sun and planets do satisfy those conditions very closely.
But not perfectly, because the planetary motions we derive by assuming the Earth and other planets are point particles are only approximately correct. The Earth, as it happens, is not perfectly spherical. Its equatorial diameter—from side to side, so to speak—is about 30 km more than its polar diameter, from north to south, owing to the Earth's spin. Thirty kilometers isn't much for a diameter in the neighborhood of 12,750 km, but it's enough to cause errors in predicted motions.
One motion that is noticeably in error is that of the Moon. The Moon deviates strongly enough from the motion predicted by Newton's laws in their simplest form that it was said to have given Newton a headache, and part of the problem is Earth's equatorial bulge.
Another such discrepancy is precession. In the nearly two thousand years between Hipparchus and Newton, science had progressed from an Earth-centered universe to a Sun-centered one, so precession could no longer be interpreted as an extra motion of the celestial sphere around the Earth. Rather, it had to be an additional slow motion of the Earth itself.
To see what that motion looks like, let's first consider the Earth's daily rotation. From the Earth, the distant stars are seen to revolve once in a little less than 24 hours; hence, from the distant stars, it must be the Earth that is seen to rotate once in a little less than 24 hours. This rotation has an axis of symmetry, which passes through the north and south pole.
The sky has poles, too. If we extend the Earth's axis beyond the north pole, it points in the direction of the north celestial pole, or NCP. (The NCP is a direction, not a specific location, because the sky really isn't a shell surrounding us, but extends for enormous distances in all directions.) And the extension of the axis beyond the south pole is the south celestial pole, or SCP.
We often hear that the Earth's axis is tilted. Usually, tilting means "not straight up and down." But in space, there is no up or down. So what does the tilt of the Earth's axis really mean? It means that the Earth's axis isn't perpendicular to its orbit around the Sun, but deviates from the perpendicular by an angle of about 23.4 degrees. (See Figure 1.)

Notice that the Earth's north pole always points in the same direction, but in December, that direction is away from the Sun, which is why the northern hemisphere then has winter. In June, that direction is toward the Sun, so the northern hemisphere has summer. (The seasons are reversed for the southern hemisphere, for what I hope are obvious reasons.)
As far as Figure 1 goes, it was right in Hipparchus's time as it is today. But there is more to the universe than the Sun and Earth. In particular, there are the stars. The Earth's north pole points roughly at a fairly bright star, aptly called Polaris. Since the Earth's axis doesn't change its direction, it points to Polaris whether it's June or December.
Once upon a time, though, it didn't. Even today, the axis misses Polaris by about three-fourths of a degree, but in Hipparchus's day, it missed it by nearly 10 degrees. That means that Hipparchus would never have used Polaris as the pole star.
It also means that the Earth's axis doesn't really always point in the same direction, but moves around extremely slowly. It's always tilted from the perpendicular by around 23.4 degrees (give or take a degree or so), but its direction sweeps around in a broad circle, exactly as Hipparchus had guessed, completing a cycle in about 25,780 years. (So Hipparchus did a pretty good job, all things considered.) That means that in 12,890 years (half of 25,780), the axis will have swept around half a circle, and Figure 1 will be wrong: The Earth's north pole will point toward the Sun in December, and away from it in June. It is this motion which Hipparchus identified as precession.
But we still haven't explained why the Earth's axis moves as it does. Newton's explanation, as given in his massive work, the Principia Mathematica, is a bit abstruse for most readers, so the irresistible tendency is to make some familiar analogy, the most common being that of a top. Everyone knows that when you spin a top, the axis doesn't remain perpendicular to the table it spins on, but instead sweeps around in a broad circle, completing a cycle in rather less than 25,780 years, and we say that the top precesses.
Being right, however, does not make an analogy actually useful. Just seeing the top precess doesn't actually improve your understanding of precession. It makes it less mysterious, conceivably, but not more understandable.
Worse still, the analogy doesn't quite fit. If you spin a top with your right hand in the usual way, the top spins clockwise as seen from above, and its spin also precesses clockwise as seen from above. The opposite happens if you spin it with your left hand—both the spin and the precession are counter-clockwise as seen from above. Either way, they're in the same direction.
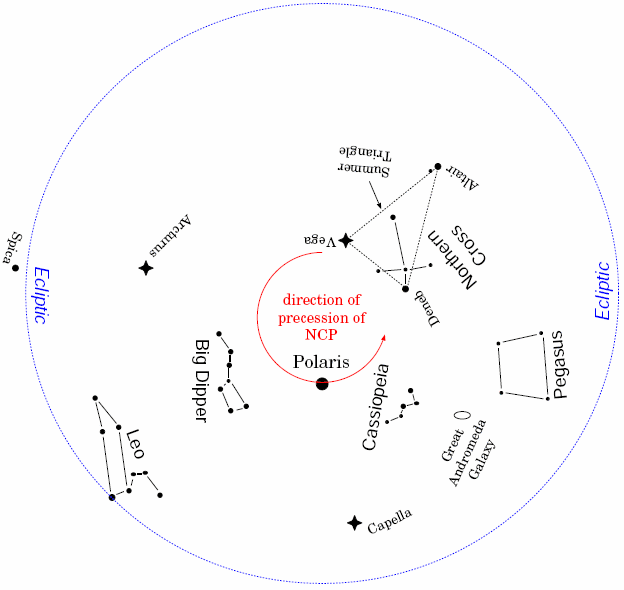
As the Earth's axis precesses, the NCP traces a path that runs counter-clockwise when we look up at it in the sky, as shown in Figure 2. That means that the Earth's axis precesses in a clockwise direction when we look down on it from above the north pole. But the Earth's spin is not clockwise. It rotates from west to east, so its spin is counter-clockwise as seen from above the north pole. The top of the world precesses the wrong way!
But why? If the same principle is at work in both the top and the Earth, why do the spin and precession work in the same direction for the top, but in opposite directions for the Earth?
We get a clue if we look at what happens in either case if there is no spin. If you don't spin a top, but just put it down on a table, it doesn't remain standing. The Earth's gravity is a destabilizing influence, and as soon as the top begins tipping over, just a little, gravity pulls it down faster and it comes to rest on its side.
On the other hand, the Moon's orbit is roughly in the same plane as the Earth's orbit, so over the course of a month, the Moon "tries" to pull the Earth's bulge back into that plane. In other words, the Moon's gravity is a stabilizing influence, not a destabilizing one, and that, as it turns out, makes all the difference.
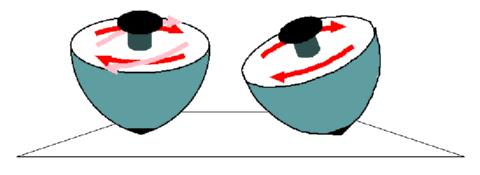
Figure 3 shows a simple top. On the left, it is drawn tipped over toward us, so that the back half of the disc is higher than the front half. We show it turning clockwise, the direction it spins if you give it a twist with your right hand. Thus, the red arrow on the back of the disc is pointed to the right, and the one on the front of the disc is pointed to the left.
Because the top is not centered over its fulcrum, the Earth's gravity tends to tip it over further—to make the higher parts in back even higher, and the lower parts in front even lower. So the motion of the top is not exactly to the right in back and to the left in front. Instead, the back goes mostly to the right, but a little upward, too, while the front goes mostly to the left, but a little downward, too. This is indicated by the pink arrows.
The top, however, is rigid. So long as it's pointed upward, there's no way to have the back go a little up and the front go a little down, in addition to spinning around clockwise. The only way for it to respond to the Earth's gravity is for the top to change the direction of its axis slightly. If we transfer the pink arrows to the diagram at right, we see that in addition to tipping mostly toward us, the top also tips a little to the left. Another consequence of the top's rigidity is that the tilt of the top only gets deflected to the left. The fact that the top holds itself together keeps it from tipping further downward.
Now that the top is tilted toward us and slightly to the left, imagine sliding clockwise around the table, so that the top is again tilted directly toward us. Following the same line of reasoning as before, the tilt must change again, tilting once more to the left. A moment's consideration will show that the process must repeat continually, so that the axis of the top will continue moving to the left (if the top is pointed toward you). Equivalently, the axis precesses clockwise, as seen from above—the same direction as the top's spin.
The situation with the Earth, however, is different. Figure 4 shows the Earth, with its axis tipped toward us, so that the back part of the equatorial bulge is "above" the orbital plane (as seen from a north-centric perspective), and the front part "below." The Earth rotates west to east, which is counter-clockwise as seen from above the north pole.
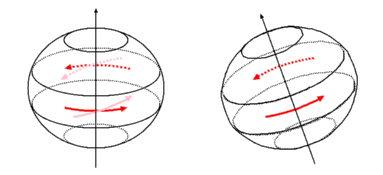
As I said above, the Moon orbits mostly in the same plane as the Earth does. Thus, the Earth's axis is typically inclined in the neighborhood of 23.4 degrees to the Moon's orbital plane. (The actual value can vary up to about 5 degrees from that average.) As the Moon orbits the Earth, it acts to bring the Earth's bulge back into that plane. You might think that when the Moon is on the same side of the Earth as the axial tilt, it acts to destabilize the Earth, but this is a product of our north-centric thinking. Conceptually, the Moon doesn't pull on the axis. It pulls on the bulge. And in any event if the north pole is on the same side of the Moon, the south pole must be on the opposite side (and vice versa).
Now, in Figure 4, without the stabilizing influence of the Moon, the back part of the bulge would be moving directly leftward, and the front part of the bulge directly rightward, like the top but in the opposite directions. In this case, however, the Moon's gravity does not tip the Earth's axis over further, but rather "tries" to bring it further upright (with respect to the orbital plane). This tends to lower the back part of the bulge and raise the front part. The impact on the direction of the arrows is that the back arrow points mostly to the left, but a little bit downward, and the front arrow points mostly to the right, but also a little bit upward. The only way to explain this with a rigid Earth is that the tilt is adjusted slightly to the left, from our perspective.
Continuing this reasoning around the Earth, we find that its axis must precess clockwise as seen from above the north pole, just as with the top, even though the Earth and top spin in opposite directions. And the reason for that lies entirely with the nature of the perturbing force: the Earth's gravity would act to tip the top over if it weren't spinning, but the Moon's gravity would act to bring the Earth more upright if it (the Earth) weren't spinning.
Of course, it must be remembered that the Moon's stabilizing influence is very slight, compared to the huge mass of the Earth. Even if the Earth had a bulge without spinning, it would take a very long time indeed for the Moon's gravity to bring that bulge in line with the orbital plane. The upshot is that the precession of the Earth's axis is correspondingly slow.
The difficulties involved in figuring out just how slow the precession was led Newton to include in his computations a number of spurious factors for which he had no logical basis. He was convinced that his explanation was essentially correct (which it was), and he must have been annoyed that the figures didn't come out quite right. Some of the problem lay in the inaccurate figures for the mass of the Earth and Moon (and to a lesser extent in their sizes and distance from each other), but some of it also lay in the fact that he didn't quite have a handle yet on how to deal with sizable mostly rigid bodies like the Earth. He didn't know how the various problems were distributed…so he just guessed.
Nowadays, that would be considered unconscientious fudging, but the Principia Mathematica was the very first work of its kind, a mathematical treatment of almost the whole of dynamics, the branch of physics having to do with motion. Neither Newton nor anyone else had more than the barest notion of significant figures or of the treatment of experimental error. It doesn't really reflect poorly on him or his work.
Besides, let he among us who is without sin (or insufficient error handling) cast the first stone!
Copyright (c) 2005 Brian Tung