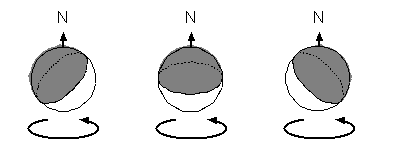
Figure 1. The celestial globe, seen from different angles.
An ingenious arrangement called a Planisphere, upon which the stars for any evening of the year are, by turning a circle, brought into view.
—from the Pall Mall Gazette, 1887
ONE OF the first things that beginning amateur astronomers are forever being told to get is a planisphere. This device allows one to determine, at a glance, what's up in the sky, and it's a great way for beginners to learn the stars and constellations. It requires no batteries or other equipment, it's light and portable, and best of all, at about $10, it's inexpensive. In spite of all this, at any sky party I've been to, most people are not using them and in fact don't own them at all. I don't use one myself, though I do have one at home. [1]
What gives? I can only guess at the intentions of most of the sky party attendees, but I suspect that human nature being what it is, people are eager to use the "real" (and expensive) astronomical tools—telescopes, CCD cameras, or at the very least, binoculars. Moreover, naked eye astronomy isn't fulfilling enough or gadgety enough, I suppose, to satisfy the tastes of many of the people who visit the parties. So perhaps planispheres get more use from the casual observers, who look at the night sky on their own, but don't consider getting together with other observers to be a suitable social activity.
Whatever the reason, the planisphere is a unjustifiably neglected instrument. In this month's column, we'll take a look at how to use the planisphere, and the principles behind its construction. As a side tour, we'll also consider the long-term effects of precession and how it too can be reflected in a planisphere.
The planisphere has a long history behind it. It was originally developed by the Greek astronomer Hypatia, who lived from about A.D. 355 to 415. She was also responsible for the development of the astrolabe. Since for most of human history, celestial navigation has been considered more important than amateur astronomy as a hobby, the predominant tool of these for most of the time since Hypatia has been the planispheric astrolabe. (There are also linear, spherical, and mariner's astrolabes, too, in case you were wondering.) Hypatia was the last great scientist of the Greek era and a passionate defender of scientific learning. For this and the crime of being non-Christian, she was murdered by a mob who pulled her from her carriage as she was on her way to teach a class, and flayed her flesh from her body with abalone shells. There is some evidence that suggests that Cyril, the bishop of Alexandria (where the great Library was situated), was responsible for her death, but this is unclear.
So what exactly is a planisphere? A planisphere is a small map of the heavens printed on a circular piece of paper or plastic about eight inches wide (different models vary). I recommend the plastic ones; they're dew resistant and will stand up to much more physical abuse than the paper ones. There are also planispheres that have glow-in-the-dark stars, ostensibly for use in the dark. Avoid these, as the glow-in-the-dark paint tends to blob and the star patterns are not as accurate. If you have trouble seeing the stars on the planisphere, use a red flashlight instead.
This circular map is mounted inside a mask that only shows part of the map at any time, just as only part of the heavens are visible in the sky at any time. (In fact, since at any moment at night you should be able to see roughly half of the sky, the mask exposes half of the star map on the planisphere.) Strictly speaking, the placement of this mask varies according to the observer's latitude, but most of the United States, for example, can use a planisphere designed for 40 degrees north latitude. Nonetheless, if you can find a planisphere better tailored for your particular location, get it!
The planisphere can be turned to reveal different parts of the sky, to simulate how the sky looks as the year progresses, or as the hours pass on any given night. Accordingly, there is one scale for the hour of the day, and another scale for the day of the year. If you turn the planisphere so that the correct hour (use standard time) matches up with the correct day, then the mask should reveal the proper appearance of the sky at that time. Depending on which direction you are facing, you may have to change the orientation of the planisphere to match what's in the sky with what's on the planisphere; holding it in its ordinary upright position shows you the sky as it appears when you face south.
For example, let's suppose that you plan on doing some stargazing at about 9:00 p.m. on November 12. It doesn't matter what year it is—the star patterns repeat themselves each year. Simply match up 9:00 p.m.—it's standard time so you don't need to correct it—with November 12. The mask now reveals the stars that are up.
Holding the planisphere upright and facing south, we see that mostly dim constellations are up in that direction. Cetus the Whale is most prominent, with Pisces the Fish and Aries the Ram just above. Cetus contains Mira, probably the second best known variable star. The best known variable is Algol, or beta Persei, and it turns out that it is a perfectly ordinary star, which just happens to be orbiting with another, darker star. Every 5 days or so, this second star eclipses Algol, reducing the total amount of light we see from this system.
Mira, on the other hand, is an intrinsically variable star. Over a period of about 11 months, it varies between magnitude 3 and magnitude 10, a swing of about 7 magnitudes. This works out to about a factor of 600 in brightness! It is the namesake of an entire class of variable stars.
Now turn the map clockwise, so that the western sky is at the bottom. We see that the Summer Triangle—a bright asterism composed of Vega in Lyra the Lyre, Deneb in Cygnus the Swan, and Altair in Aquila the Eagle—will soon be setting. Though it's called the Summer Triangle, it actually remains visible well into December, because even though the Summer Triangle sets earlier and earlier each night, so does the sun at this time of year. Since the night begins earlier, then, the Summer Triangle almost seems to stop its daily advance.
Turning the map clockwise again, we can examine the northern sky. We see that Cassiopeia the Queen is high in the sky, looking more like an M than her trademark W. To her lower left is Cepheus the King. One of the stars that may be labelled specially on your planisphere is delta Cephei. This is a variable star of a special class, named Cepheids, whose actual brightness varies in a precise period. What's more, this period is strongly correlated with the average brightness, making these stars very effective for determining the distance to other galaxies. Astronomers watch for Cepheids in these galaxies, determine their period, and work out their average brightness. Since their apparent brightness depends only on their actual brightness and their distance, that distance can be worked out quite easily.
Finally, turning the map clockwise once again reveals the splendid eastern sky. Here, the constellations of winter are rising, and these are among the brightest in the sky. Orion the Hunter, with his bright belt of three stars, usually outshines all but the brightest of light polluted skies. Rising ahead of him is Taurus the Bull, home to the Crab Nebula and the Pleiades Star Cluster. In the months to come, you'll see Canis Major the Great Dog, with Sirius, the brightest star in the night sky.
Looking around the time and date scales on the planisphere, you'll notice that the same sky is visible throughout the year, just at different times of day. This same sky, for instance, is visible about two weeks later at 8:00 p.m., as you can easily verify by looking at the time scale for that date. Of course, this sky is sometimes visible only during the day, when the sun drowns it out.
Nevertheless, the simple manner in which the sky changes from day to day and hour to hour is what makes the planisphere possible. The stars can be imagined to be placed on the inside surface of a great celestial sphere with the earth and all of us at the very center, and this is in fact how many of the ancient and medieval astronomers saw the sky. In fact, there are such things as celestial globes, which show the stars on a celestial sphere, only from the outside. One result of seeing the globe from the outside is that all of the constellations are mirror-reversed. Imagine if you were on the inside of a terrestrial globe—you'd see the United States backwards, for instance, with the Florida peninsula extending to the lower left and New England at your upper left.

You can buy celestial globes even today. Like ordinary globes, they pivot at the poles, with Polaris at the north. (See Figure 1.) At any date in the year, at any specific time of night, only half of this globe can be seen in the sky. Figure 1 reveals that the part of the sky nearest the north pole is visible each and every night. This portion of the sky is called circumpolar, and if you turn your planisphere through a complete cycle, you'll notice that these stars are visible no matter how you turn the dial, so that they seem to circle the pole, hence the name.
At the other end of the globe, near the south pole, the stars can never be seen. This will be harder for you to verify, but some of the constellations near the south pole are called Octans the Octant and Centaurus the Centaur. You will note that no matter how you turn the dial, these constellations never show up, and that is because they can't be seen from most U.S. latitudes. (Other countries at other latitudes will naturally have a different set of constellations they can't see.)
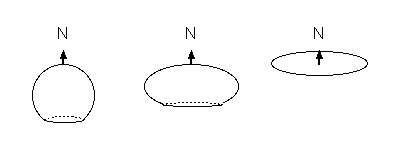
Suppose that we cut off the portion of the sky that we can't see—after all, it's no use to us. (See Figure 2.) We now have something that looks a little like an overgrown umbrella, or a modern art lamp shade. Now imagine pulling the lip of this truncated globe up, flattening the globe out. Instead of spinning the globe to see what's up in the sky out, we turn the disc. This is exactly what the planisphere map is—it's a flattened truncated celestial sphere.
The problem with flattening out a sphere, as any fan of maps knows, is that you inevitably have to distort the map. There is no way to display the spherical sky on a flat piece of paper without getting some of the distances wrong. Any way of doing it is a compromise—you can get some parts of the sky to look nearly perfect, but some other parts will suffer for it. The trick is to define the way you do this, called a projection, in such a way that no single portion of the sky suffers too much.
On a terrestrial globe, the grid lines are called lines of latitude and longitude. On a celestial globe, the corresponding lines are called lines of declination and right ascension, sometimes abbreviated to RA. A projection can be defined in terms of how these lines are mapped onto a flat piece of paper.
Because a planisphere spins around the north pole, where the lines of right ascension meet, these lines of right ascension must be straight and evenly spaced rays spreading out from the center pivot, where Polaris is. Otherwise, the outline of where the horizon is each night would change as you turned the planisphere. In the same way, the lines of declination must be mapped as concentric circles spreading away from Polaris. But unlike the RA lines, these circles do not have to be evenly spaced. The spacing of the circles of declination is the freedom we have in defining our projection.
One way to arrange them is to space them equally. This is called the azimuthal equidistant projection, and it is reasonably accurate near the pole, but becomes increasingly distorted as you proceed toward and beyond the celestial equator. This results in constellations such as Scorpius the Scorpion being stretched nearly out of recognition. Because planispheres don't have to show the whole sky, they typically use this projection anyway. It's also used in the polar portions of some star atlases, because the equal spacing makes it relatively easy to interpolate the positions of objects between grid lines.
Another way to arrange them is to space them in such a way that all angles are preserved at any place on the map. Such a projection is called stereographic, and it spaces the lines of declination wider apart the further away you get from the poles, so that the scale varies from point to point, but the constellations look much more recognizable. Few planispheres use a stereographic projection; I don't believe any current ones do.
Regardless of the projection used on the planisphere, the hole is cut according to the relation
where l is the latitude which the planisphere is designed for, a is any given line of right ascension, and d is the declination of the horizon at that value of right ascension. For the rather special case of l = 45 degrees, the above equation reduces to
If you plan to make your own planisphere, the easiest thing to do is probably to use the azimuthal equidistant projection and then d is linear with distance from the center of the planisphere map disc.
For centuries many societies have placed a special privilege on Polaris, as the star around which all other stars revolve—at least, for observers in the northern hemisphere. The name Polaris means pole star, in fact. But it has not always been the pole star. There is an unaccountably popular belief that Polaris is the brightest star in the night sky—which it isn't—and that there is something about being the pole star which confers special privileges upon it—which there isn't. If there are Polarisians, they have not the slightest idea that the earth's north pole points to it—more or less.
That's part of the story, you see. Polaris is very close to the north celestial pole, but it is not precisely there. If you examine a picture of star trails, you'll notice near the center a very bright streak. That's Polaris. It moves very little throughout the night, but move it does. That's because it's displaced from the pole by about 45 minutes of arc—about three-quarters of one degree.
The point about which the star trails revolve is simply the direction in which the earth's north pole points, and that's called the north celestial pole. We northern hemisphere observers should be thankful that Polaris is even so close. In the southern hemisphere, the nearest star to the south celestial pole is sigma Octantis, and that is a poor fifth-magnitude star. It's not even as close to the pole as Polaris is to the north pole; sigma Octantis is off by about one full degree.
What's more, Polaris used to be much further from the north pole. Or more accurately, the north pole used to be much further from Polaris. The earth is tilted about 23.5 degrees from the ecliptic, which represents the plane of its orbit around the earth. As a result, at certain times of the year, its north pole is tilted toward the sun and its south pole away from the sun, and the northern hemisphere gets summer and the southern hemisphere gets winter. Six months later, on the other side of the orbit, exactly the reverse is true. In between, the poles point "toward the side," and it's springtime or fall. But the tilt itself remains constant; it's only the relationship of that tilt to the position of the sun that changes.
It just so happens that this tilt right now has the north pole pointing toward Polaris. But over the years, this tilt actually changes, swinging in a broad circle, so that thousands of years from now, the earth's north pole will tilt 23.5 degrees in precisely the opposite direction, 47 degrees from Polaris. After thousands more years, the tilt will swing back again and Polaris will once more be the pole star.
This entire cycle takes about 25,800 years, during which the pole sweeps out a circle 47 degrees across. Such a slow cycle seems that it would take a long time for mankind to determine. Remarkably, though, we've known about it for over 2,000 years.
Our story begins in about 300 B.C., when a Greek astronomer in Alexandria, named Timocharis, created one of the earliest known star catalogues. Not much is known about this catalogue, but a much more prominent Greek astronomer, Hipparchus, consulted it when creating his famous star catalogue in about 130 B.C., the one that would eventually make it into Ptolemy's famous compendium, the Almagest. In examining the catalogue, Hipparchus noticed that the positions of the poles and equinoxes had changed relative to the background stars as recorded by Timocharis.
Now it would have been easy to conclude that Timocharis had simply made errors, and that the pole had really remained constant over those 170 years or so. But Hipparchus was a careful astronomer, and he consulted a number of different star catalogues compiled in the intervening period. He determined instead that the old maps were basically correct, and that the earth had really "wobbled" slightly during that time. Hipparchus is then generally regarded as the discoverer of precession, which is the term used for this wandering of the poles.
Despite discovering precession, Hipparchus hadn't the slightest idea what caused it. The general conception of the stars back then, as we described earlier, was that they were attached to a giant globe, which turned around the earth once in a little less than one day. As a result of precession, the model changed slightly, so that the stars were still on the inside of a giant globe, and there was still a globe that turned around in slightly less than a day, but now they were two different globes. The stars were now attached to a globe that turned once every 25,800 years or so, and this globe was in turn attached to a globe that spun once every day or so.
(Astronomers would later believe that even the precession rate itself varied over the years, and this effect, termed trepidation, required yet another globe between the other two globes. But that's a story for another day, not the least because trepidation doesn't exist.)
This model worked, insofar as it predicted future and past changes in the motion of the stars, but it hardly served as a physical explanation of those changes. Such an explanation of precession would have to wait until Isaac Newton and his law of universal gravitation. Because of the earth's spin, it bulges slightly at the equator—its "width" is ever so slightly larger than its "height." Newton discovered that even this slight bulge means that the sun and moon do not tug at the earth in a uniform manner; the earth has handles that the sun and moon "grab onto," so to speak. Together, they cause the earth's axis to wobble in precisely the manner that Hipparchus had discovered over 1,800 years before. (Well, not precisely. The other planets also contribute to the precession, but their contribution is so many decimal points less significant that it matters not one whit to us here.)
There was a reason I told this long story.
It turns out that we can design a special kind of planisphere that accounts for not only the daily motion of the stars, but also precession. The way that we'll represent precession in our second planisphere is to use two discs—one in back of the frame, and one in front. The disc in back will be the map disc and will rotate around the center of precession. The disc in front will actually contain the mask that represents the horizon. Thus, instead of turning the map behind the mask, we'll spin the mask in front of the map. (You can convince yourself that these two are really equivalent, using an ordinary planisphere.) These two turning discs are a two-dimensional version of the nested celestial globes.
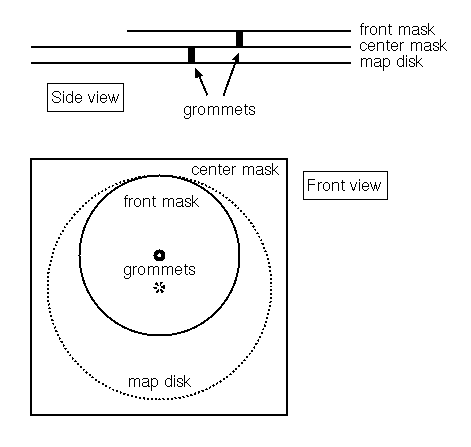
You can download the parts necessary to create this planisphere here. Included are front mask parts (left and right), center mask parts (left and right), and the map disc with brief instructions (here). Assemble as indicated, laminate, and fasten with pivoting grommets. (See Figure 3.)
To make things simple, I assumed a latitude of 45 degrees; I also assumed that December 21 is always the winter solstice. I welcome comments from any readers who might know the exact convention that should be used here. Also, because the map disc is no longer centered at the current north pole, the horizon is not exact here, but is instead inaccurate for some times of day. However, the sky shown should be approximately correct at any moment. Rotating the rear map disc simulates the changing of the skies due to precession. [Note: The map disc is currently not labeled for the number of years into the past or future required to precess by a given amount. I'll update the PostScript files accordingly and announce the change on sci.astro.amateur.]
Note that in our precessing planisphere Polaris is not missing as in ordinary planispheres, but is plotted in its full, second-magnitude splendor, since it's no longer the pivot of the map. That duty now falls upon the ecliptic pole, which is at 18 hours (270 degrees) right ascension, 66.5 degrees north declination. Which leads one to ask, is there anything of import at that location? A quick look at our map disc reveals no star down to fourth magnitude there; in fact, there is no star as bright as sixth magnitude within even a few degrees.
But there is something notable there just the same. Within about a fifth of a degree, much closer than Polaris is to the current, ephemeral pole, is NGC 6543, otherwise known as the Cat's Eye Nebula. It's a planetary nebula, the dying remains of a sun-like star. It's about ninth magnitude and through a moderate-sized scope looks something like the inside of a marble, hence the name. It also has one of the brightest central stars of any planetary nebula, about magnitude 11.4. The next time you get out under the skies, take a peek in that direction and consider the slow motion of the earth around which it centers. Clear and steady skies, and happy observing!
[1] Since I first wrote this, I've acquired a spiffy new planisphere. It's not for everyone, but it is a splendid piece of work. Check it out.
Copyright (c) 1999 Brian Tung