Figure 1. Orbits of Venus and the earth.
I cannot, by the progress of the stars, / Give guess how near to day.
—Julius Caesar, Act II, Scene i
I WAS, as I've mentioned in other places, away from astronomy for a long period of time, between the ages of 10 and 30, more or less. I don't mean to say that I was ignorant of astronomy, or even that I had no idea what advances NASA was making, for example. But for those 20 years I didn't much care if it was cloudy on a moonless night, or if atmospheric turbulence made even the planets twinkle, or if the sky was studded with as many as a couple of dozen stars.
Then my wife bought me a telescope for Christmas, a 4-1/2-inch reflector from Orion. That was a decent step up from the 60 mm department-store scope so often vilified by serious amateurs and you might imagine that that started me on the way back to active observing, but it didn't.
Two and three years later, the two great comets of the latter 20th century, Hyakutake and Hale-Bopp, made their prominent appearances. Hale-Bopp in particular was well-placed for evening viewing and at its best was impressive even through the Orion reflector in light-polluted Santa Monica. Again, you might imagine that this dramatic event would kick me in the pants, astronomically speaking, but it didn't.
When I finally realized that I wanted to, needed to get back into the astronomy swing of things, I wasn't seated at a telescope. It wasn't even nighttime. Instead, I was sitting and eating a burger in a diner, reading a magazine. The time was late 1997, the magazine was Astronomy, and the article—
But now I'm getting ahead of myself. I should start at the beginning…
The first person we know of who determined some kind of a distance to a star was Aristarchus. He lived between 310 and 230 B.C., and he determined from tracing the shape of the earth's shadow during lunar eclipses that the earth was about 3 times larger than the moon, which is about right. He also determined, by measuring some angles, that the distance to the sun was at least some 20 times the distance to the moon. If so, he concluded, then the sun must be at least 7 times larger by diameter than the earth. A drastic understatement, but let's remember he was working without a telescope or precision equipment.
Before Aristarchus died, another Greek, Eratosthenes, determined that the earth itself was about 13,000 km across, meaning that the sun must be at least something like 90,000 km in diameter. Simple trigonometry, based on the apparent size of the sun, suggested that the sun should therefore be about 10 million km away, a monstrous distance.
It hardly made any sense to Aristarchus that the huge sun should circle the tiny earth, so he proposed that it was the sun that was at the center of the universe, instead of the earth, which he believed revolved around the sun like all of the other planets.
The greatest of the Greek scientists, Archimedes, wrote about Aristarchus's idea and rejected it almost immediately, since it's patently obvious to even the greatest simpleton that the sun revolves around the earth and not the other way around. Furthermore, if the earth were moving, Archimedes argued, we should feel ourselves being thrown this way and that as the Earth changes direction, just as we feel ourselves thrown to the outside when riding in a vehicle making a tight turn.
Finally, if the earth were really moving around the sun, then we should see the stars move in little circles throughout the year—an effect called parallax—and since they plainly don't, the earth simply couldn't be moving around the sun. You can see this by moving your head back and forth and watching the relative apparent positions of, say, your window frame and distant buildings. The stars are much further away, to be sure, but in order for the parallax to be invisible, the stars would have to be incredibly far away, and Archimedes could see no reason for them to be that far.
Much is made of the Greek world's affinity for free inquiry, but it's often the case that inquiry is most free when it doesn't contradict obvious facts of life, and Aristarchus's case was no exception. Few if any Greek scientists would ever take Aristarchus's idea seriously, at least publicly.
The stars are so very far away, you see. Astronomy texts attempt to convey an impression on just how far by getting you to imagine the sun as a beach ball, the earth as a walnut a football field away, and so forth. It's all to little avail, as far as I'm concerned; the distances are simply too huge for us to fathom. But perhaps here's another way: if you were to add up all the distance ever traveled by every single automobile, bicycle, truck, chariot, and indeed any kind of road vehicle that has ever existed on the earth, that should just about get you to the nearest stars.
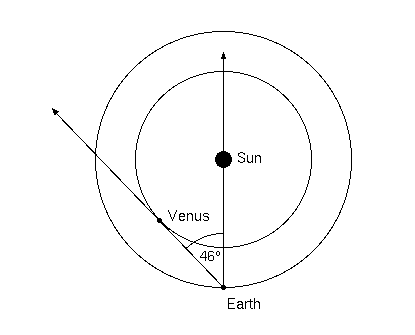
But let's suppose we try, after Aristarchus, for nearer game—our own sun. Once the heliocentric solar system was installed in the scientific consciousness, we were able to determine the relative distances between the planets. The distance from the sun to the earth was defined as one astronomical unit, or AU for short. The distances from the sun to Venus and Mercury (in AUs) in particular were easy and could have been determined by the Greeks. These two planets are closer to the sun than the earth and can only appear in the sky just so far from the sun. (See Figure 1.)

Figure 1. Orbits of Venus and the earth.
The farthest that Venus ever gets from the sun, in terms of angular distance, is about 46 degrees. (For that reason, we never see Venus at midnight.) From trigonometry, we can determine that the distance SV is related to SE by the formula
which yields a sun-Venus distance about 0.72 AU, and that is just about right. A similar method works for Mercury, too. The other planets, however, orbit the sun further away than the earth, and for them another method is required. Rather than go through that, let's fast forward to Kepler and the last of his three laws of planetary motion. That third law states that the period T of a planet's orbit, expressed in years, is related to its distance d from the sun, expressed in AUs, according to the formula
Mars, for example, takes about 2 years to orbit the sun, so for Mars, T is equal to 2; T2 is equal then to 4. What d, when cubed, yields 4? About 1.6, close enough, and Mars is in fact about 1.6 AU from the sun. (Its orbit is noticeably elliptical, so its distance varies from month to month.)
But what about the actual distance to the sun? What is the length of AUs measured in terms of something we know, like miles or furlongs or centimeters? The Italian astronomer Giovanni Cassini, for whom the spacecraft and the division in Saturn's rings is named, reasoned that if Mars were observed from two different places on earth at precisely the same time, it would appear to be in two different places in the sky—again, parallax, but this time of Mars, rather than the stars. (See Figure 2.)
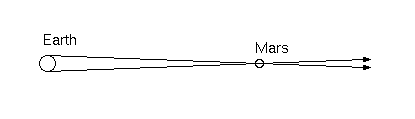
Figure 2. Parallax of Mars.
By knowing the distance between the two vantage points and the apparent change in position, Cassini could work out the distance to Mars. That experiment was carried out in 1672, by Cassini in Paris and a French astronomer, Jean Richer, in South America, and from those observations Cassini derived an earth-Mars distance of about 83 million km. Since the earth-Mars distance is about 0.6 AU, the AU itself must be about 138 million km. That's a little below the now accepted value of about 150 million km but for the first time, a sense of the true scale of the solar system was known and it was much larger than Aristarchus had ever imagined. Later measurements of transits of Venus across the face of the sun would yield much more accurate measurements of the AU. Today, the best measurements are obtained using radar measurements bounced off of other planets.
Incidentally, the Danish astronomer Ole Roemer used Cassini and Richer's value of the AU three years later, in 1675, to determine the speed of light for the first time. He used variations in the timings of the eclipses of Jupiter's satellites, along with the length of the AU, to arrive at a value of 225,000 km/s. That's about 25 percent too low, but it was the first time that the speed of light had been determined to be a large, but finite, number.
How about the stars themselves? If the method worked for Mars, couldn't it work for the stars too? The problem is that the parallax angle for Mars was already very small; the apparent change in angular position amounted to about 25 seconds of arc—about 1/150 of a degree—and if the stars were any further than about 25 AU then there would be no hope of determining stellar parallaxes with the technology of the day. It was tried and sure enough, it failed, so aside from knowing that the stars were more than 25 AU away, not much more was learned. Too bad!
But Mars also exhibits another parallax effect, called retrograde motion. It doesn't move uniformly across the heavens as the nights pass, but instead sometimes moves forward, sometimes backward. Generally speaking, it progresses west to east, but as the earth laps it every 26 months or so, it occasionally appears to move east to west. This is a result of viewing Mars from a moving platform—the earth—and it occurred to astronomers that the same effect could be used to measure stellar parallaxes. Instead of observing the stars from opposite sides of the earth, in other words, we could observe the stars from opposite sides of the earth's orbit. This expanded the base of operations from about 10,000 km to over 300 million km, an increase of 30,000 times, meaning that the distances that could be measured by means of parallax also expanded by a factor of 30,000.
The distances to the outer planets could also be worked out in this manner, by the way, but while the earth is moving, so are the planets, and the computations get more complicated. All but a couple of the stars, on the other hand, don't move noticeably over the course of a year or so, and the ones that do move do so very steadily, in straight lines, unlike the planets, whose motions are relatively complex.
Observations concentrated on those stars that do move, nevertheless, because it stood to reason that they were the closest. If you're in a crowded room, you can easily see that the people closest to you seem to pass by your field of vision relatively quickly, whereas for someone far away, it can take them quite a while. In the case of the crowded room, you can also tell that they're closer because of apparent size, and because everything's still close enough for your binocular vision to give you a true three-dimensional picture of the room.
Stars, on the other hand, vary tremendously in size, and even if they didn't, they're so enormously far away that even the closest ones are point sources as far as we're concerned. And our two eyes, providing their measly 10 cm or so of a base for parallax, can't come close to yielding a three-dimensional picture of the stellar neighborhood. So astronomers used the cue of apparent motion—in the case of stars, called proper motion—as a guide in guessing which stars might be the closest and therefore exhibit the greatest amount of parallax. (This motion is termed proper not because it's "correct," but because it's "proper" to the star itself, and not a result of the earth rotating or revolving around the sun.)
Where should a star be chosen? As the earth orbits the sun, all the stars should exhibit an east-west motion due to parallax. This motion, unfortunately, is difficult to detect because the earth rotates, meaning that all the stars move from east to west throughout the night. In order to detect an arc second of parallax, one would need a clock accurate to 1/15 of a second, for that is how long it takes a star to move 1 second of arc. In the 18th century, no such clock could be built.
What about other kinds of motion? Stars along the ecliptic only exhibit east-west motion, but stars far from the ecliptic also show north-south motion. In principle, stars at the ecliptic poles would trace out a circle identical in shape to the earth's orbit. The advantage of choosing such a star is that all stars appear to rotate strictly east to west. They should stay at the same declination, or celestial latitude. If they do happen to change declination, it was reasoned, that would have to be due to parallax. Therefore, you don't have to keep accurate time, you merely have to examine the declination of the star as it passes overhead. In the 1728, the English amateur astronomer James Bradley attempted to detect the north-south parallax of the star Eltanin (gamma Draconis) as it passed each day over a specially mounted zenith telescope. If it crossed the field of view of the telescope at a slightly different position as the months passed, that would have to be the parallax and he could thereby determine the distance to that star.
Sure enough, Eltanin passed overhead at a slightly different point each day, moving slowly but steadily southward. Theoretically, a star far from the ecliptic should reach the northernmost extent of its parallactic path when the sun is most precisely between the earth and that star in its orbit around the sun—when the star is at conjunction. On that date, that star should pass directly overhead at around noon local time. Bradley watched patiently each day as Eltanin passed further and further south, and kept right on progressing south, even as 18 December 1728, the date of conjunction, passed!
What Bradley had discovered was not stellar parallax, but what is known as the aberration of light. He saw it, but it was some time before he arrived at an adequate explanation of it, and when he did, he was sitting on a sailboat watching the weathervane move back and forth as the boat changed tack. Rather than explaining it the way that Bradley saw it, however, I'll explain it by analogy with raindrops on an automobile windshield. If we suppose that there is no wind, and the car is stationary, then the drops appear to the observer, correctly, to be falling from straight above.
If, however, we start the car in motion, then the raindrops ahead of us appear to be moving toward us, and those behind us appear to be moving away from us. The end result is that the raindrops appear to be coming from a point directly ahead of where they "ought" to be coming from. What's more, the faster we drive the car, the further out in front the raindrops appear to be coming from.
Now, the speed of light is many millions of times faster than the speed of raindrops, and the speed of the earth is only many thousands of times faster than an automobile, but even so, the effect is detectable, and is also at least an order of magnitude or so larger than parallax. Bradley had therefore proven that the earth moves around the sun, but in a way wholly unexpected by him.
What's more, whereas the parallax effect is determined by the earth's position relative to the sun, the aberration effect is determined by the earth's motion around the sun, and these two are at right angles to each other. This explains why Eltanin continued southward past the time that would have been predicted from parallax alone. (See Figure 3.)
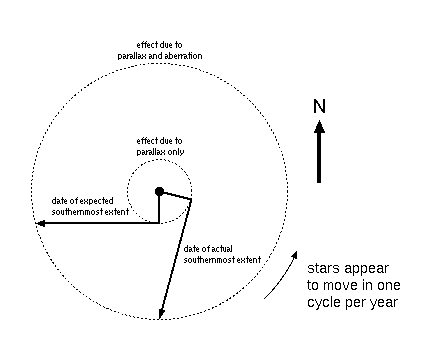
Figure 3. Effects of parallax and the aberration of light.
As you can see, the aberration effect totally swamps the parallax effect, and that's even true for the nearest of stars. As you choose stars that are more and more distant, the aberration effect remains constant, but the parallax effect grows smaller in proportion to the growing distance. Bradley was totally unable to detect the parallax of this star, and without it he couldn't determine the distance to the star, because the aberration effect, unlike parallax, is constant and doesn't depend on the distance to the star. (Eltanin is nearly 150 light years away, so it's no knock on Bradley that he couldn't find its parallax.) In fact, it's only because the aberration effect is constant that parallax can be detected at all—by determining the relative change in position that a star makes in constrast to its neighbors.
About a century after Bradley's achievement, in 1838, the German astronomer and mathematician Friedrich Bessel observed a parallax of 1/3-arc second on the star then known simply as 61 Cygni. This means that as the earth moves around the sun in its orbit, 61 Cygni appears to trace out a little oval that is 2/3 of an arc second in width. By convention, the parallax is defined as half of this width, just as the distance from the earth to the sun is half of the base from which the parallax is measured.
How far, then, is 61 Cygni? We can express this in terms of a parsec, which is the distance at which a bar 1 AU in length will appear to extend 1 arc second. That distance is equal to 206,265 AU (the number, which has an almost mystical significance to astrometrists, is equal to the number of arc seconds in 1 radian). Since the angles involved are so small, distance is inversely proportional to parallax, so that 61 Cygni must be 3 parsecs away. A parsec is equal to about 3.26 light years, so Bessel had determined the star to be very nearly 10 light years away. That's a bit of an overestimate, but pretty good for a first try, and in commemoration of this feat, 61 Cygni is now known informally as Bessel's Star.
(Actually, as is so often in the history of science, Bessel wasn't quite the first to determine a stellar parallax. Working a quarter of a world away, the South African astronomer Thomas Henderson determined the parallax of alpha Centauri, which is the closest star visible to the unaided eye, outside of our own sun, and he did it before Bessel had arrived at a figure for his star. Possibly because of his remoteness, however, he didn't publish his result until months after Bessel had gotten into print, and it's for that reason that Bessel gets the credit and not Henderson.)
Determining parallaxes is not an easy task. First of all, the image of a star, even through perfect optics, is not a point of light, but rather a small disc called the Airy disc. This disc gets smaller as the optics get larger, but even for a mirror 1 meter in diameter, the disc is still about 1/8-arc second across, and Bessel certainly didn't have access to anything that large for the purposes of determining stellar parallax.
Moreover, the atmosphere can wreak havoc with the image of a star, distorting it and moving its apparent position back and forth. The upshot is that the uncertainty of a star's position on any given night may be many times the expected parallax and it requires careful observations taken over a period of months to obtain even a rudimentary parallax measurement. For this reason, using parallax to determine the distances to the stars was a method limited to stars within about 10 parsecs even well into the 1980s.
Then the Hipparcos satellite was launched. It stands for High-Precision Parallax Collecting Satellite, and it was launched into earth orbit in order to at least evade atmospheric effects. It almost didn't make it. After a perfect launch, one of its booster rockets failed to fire properly, and instead of settling into a nearly circular orbit as planned, it revolved around the earth in a severely elliptical orbit which at its closest approach brought it within about 400 kilometers of the earth's surface. At that height, the atmosphere may begin to affect it, and it was feared at first that all was lost. Despite the near-catastrophe, Hipparcos functioned quite well and returned four years of high-precision data on 120,000-odd stars and another set of lower-precision data (but still very high by human standards) on about a million more.
It took four years more to digest the data. When it was done, accurate parallaxes had been determined for most of the top 120,000 stars, reaching out to 100 or 200 parsecs. The results are available in a 16-volume report. Volumes 5 through 9 are the so-called Hipparcos catalogue, giving detailed astrometric and photometric data for the 120,000 stars. Volumes 14 through 16 are the three-volume Millennium Star Atlas, a $250 or so "atlas to end all atlases." And finally, the whole story was written up in summary form in an article for the December 1997 issue of Astronomy, which is where I began this entire story.
My return to astronomy really began with that article, and below are the fruits of that return. The first thought I had upon reading this article was how nice it would be to have a three-dimensional map of the stars. I had just gotten through doing a prototype of a program to generate single-image random dot steroegrams, or SIRDS, which are the ancestors to those funky three-dimensional posters that you see in the malls. It occurred to me that I might easily use the same principles to produce three-dimensional stellar pictures.
It turns out that the entire Hipparcos catalogue is available on the Web. It takes a high-speed connection to download it within a reasonable period of time, but once you have it, even a computer a couple of years old can manipulate it reasonably fast. I did end up writing a program to generate the pictures, and below are some results that you can view on your browser. The inlined images are regular 2-D pictures; clicking on them will bring up the 3-D stereograms. At the end is a link to a form which allows you to generate your own stereograms of whatever portion of the sky you wish.
Note: I get much better results when I view these pictures with a "helper" application than I do using Netscape to view them. Your mileage, as always, may vary.

Our first example is the Big Dipper, the brightest part of Ursa Major. It consists of seven stars in the shape of a dipper, or plough; and its name in the U.K. is the Plough. Normally, constellations or asterisms are chance collections of stars. That is, they are not physically associated, but are merely along the same line of sight, just like if you put your thumb in front of the moon does not make it physically associated with the moon.
Not so with the Big Dipper. Out of the seven stars that make up the Dipper, the central five are in a loose association, some 80 to 90 light years away. Only the outer two, Benetnasch (eta Ursae Majoris) in the east (upper left here), and Dubhe (alpha Ursae Majoris) in the west (lower right here), are not part of this group.
The stereogram here (click on the above image to retrieve it) illustrates this fact. If you fuse the left image with your left eye with the right image with your right eye, you'll see a stereo image that shows the central five stars of the dipper hanging closer than the outer two.

The Pleiades are perhaps the most famous open star cluster. Open clusters are groupings of stars that are newly born. Typically we see the brightest of them, which are hot blue stars destined to live only a few tens to hundreds of millions of years. Occasionally some of them have already outgrown their normal lifetime and are swelling into the red supergiant phase, after which they will blow themselves up as violent supernovae.
Also called the Seven Sisters, only six of the Pleiades are easily seen by the average naked eye, though some sharp-eyed observers can see more than a dozen. It helps to be experienced enough to know where to look for the dimmer ones. While pictures of the Pleiades show some nebulosity enveloping the Pleiades (once thought to be the cloud from which they were born, but now thought by some to be a chance cloud in their path), it's actually quite difficult to see, and most telescopes will show only the stars themselves. To see if you might be seeing the nebulosity, check with the Hyades, to the southeast of the Pleiades, in the direction of Aldebaran in Taurus the Bull. If you see it there, too, then you're not really seeing it; the Hyades are not swathed in nebulae.
In this view here (click on the above image to retrieve the stereogram), we have moved by 95 parsecs, or about 310 light years, in the direction of the Pleiades, in order to show more detail in their spatial placement. The brightest star, near the middle, is still Alcyone (eta Tauri). Estimates place the population of the Pleiades at over 100 stars.

If it weren't for the Pleiades, the Hyades would be the most famous open cluster in the sky. They mark Taurus the Bull's snorting visage, and are marked in the sky by the Bull's red eye, Aldebaran. Aldebaran only looks as if it's part of the Hyades; in reality, it is a foreground star only a mere 20 parsecs (about 65 light-years) away.
But in this view, we haven't shown the Hyades as they appear from earth. Instead, we've moved about 15 parsecs (about 50 light-years) in the direction of Orion's shield shoulder. In addition, we are looking sideways, so that east is up and west is down. This allows us to show the separation between the Hyades and Aldebaran when they are looked at obliquely; the Hyades are at the top, and Aldebaran is actually the very bright star at the bottom. In between, actually, are the more distant Pleiades.

The Coma Berenices Star Cluster has to be distinguished from its larger but somewhat lesser-known neighbor, the Coma Berenices Galaxy Cluster. The latter is a target only for larger telescopes, but the Star Cluster can be seen by the naked eye under reasonably dark skies. Binoculars will display it in all its splendor, the brightest stars looking like jewels in the sky.
The cluster is supposed to represent a head of hair. Some people consider the resemblance obvious; others consider it obviously a sign of mental disturbance. The view here (click on the above image to retrieve the stereogram) reveals how the cluster would look if we were to approach it by 35 parsecs, or about 115 light years. This view reveals most of the bright stars in the cluster to form a true open cluster, rather than a chance alignment.
I've set up a page whereon you can make your own stereogram. The images look just like the ones here, except that you can pick your own coordinates, your own magnification, and select more or fewer stars based on apparent visual magnitude. You can even move out into space! (This form is no longer operational, unfortunately.)
This peculiar-sounding question is asked by the Morrisons in the October 1998 issue of Scientific American, in the Wonders column. I've made some similar maps of the sky from a hypothetical planet around 47 Ursae Majoris.
Copyright (c) 1999 Brian Tung