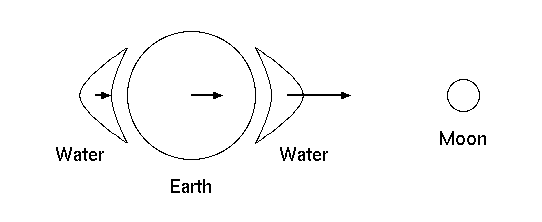
Figure 1. Lunar tides (not to scale).
They would make men believe…that the Moon is made of Green Cheese.
—John Frith
WHEN I was about nine years old, my parents bought me an optics set for Christmas. It was ostensibly from Santa Claus, but at that age, you are beginning to feel a little wise and skeptical, and look down upon the credulous fool you used to be. So I was fairly certain that my parents had obtained the set in a more mundane fashion, from Edmund Scientific.
The set contained a prism and 8 to 10 lenses of various kinds, as well as a short book which explained how to build telescopes and other interesting devices. My first project was the Galilean telescope, which unlike any other telescope today uses a concave eyepiece. This produces an upright image but a very small field of view—Galileo's specimen only had a 12-minute wide field of view, about the width of a strand of spaghetti held at arm's length.
But my lenses yielded a shorter tube and hence a wider field of view than Galileo had, and the upright image was useful for spying on distant billboards, electrical warnings on telephone pole transformers, and of course people too. I didn't live near any girls, though, and in any case I was only nine, and while I had outgrown Santa Claus, I hadn't entirely shuffled off my distrust of girls.
So it was inevitable that I would find something else of interest to look at, and one night, after discovering that the telescope would not allow me to read distant writing in dim light, I turned the paper towel roll—for indeed that was the tube body specified by the Edmund Scientific manual—toward the one object that was like no other in the night sky—the Moon. For about an hour, I sat transfixed in my lawn chair, wondering at all the things I could see. It is a source of endless fascination, even now.
So let's consider the Moon. The word itself is from Middle English moone, which in turn derives from Old English móna. It has always meant "moon," though it has been spelled variously mone, mon, mowne, moyn(e), mwne, mune, muin, as well as its current spelling and the two already mentioned. Before Old English, the history of the word becomes hazier. There is a plausible story that the ultimate root is Indo-European me-*, "to measure," since the Moon "measures out" one month, but that is far from confirmed.
The Oxford English Dictionary defines "moon" as "The satellite of the earth; a secondary planet, whose light, derived from the sun, is reflected to the earth and serves to dispel the darkness of night." This poetic passage, perhaps not what one might expect from a dictionary, gives the romantic impression that the moon (which I will write in lower case from here on out) protects the earth from total darkness by passing a shaft of reflected sunlight, taking care through the night to maintain that beam on the shrouded earth.
The truth is a bit more prosaic. The moon does in fact reflect sunlight toward the earth, sure enough, but it reflects sunlight in all the different directions, some more than others. The only direction in which the moon reflects absolutely no sunlight is directly behind it (from the point of view of the sun). There the moon serves only to block sunlight.
One somewhat surprising fact about the moon is how small it is. Nearly no one guesses that it would take nearly 200 full moons, stacked end to end, to reach from the horizon to directly overhead. Possibly the impression of greater size has to do with all those movie posters with two silhouettes projected against a full moon. Another fact which bypasses the attention of many people who ignore the moon is that half the time it is not in the night sky at all. Such people are surprised to hear that you can actually see the moon during the day. It is easy to see at about first quarter and last quarter, when it is about 90 degrees displaced from the sun. Too close to new moon, and it is lost in the glare of the sun. Too close to full moon, and it is diametrically opposite from the sun, and then it truly does rule the night sky, from dusk till dawn.
The moon is a tantalizing astronomical target for the unaided eye. To us modern observers, who know about craters and the utterly alien surface from the Apollo landings, the moon has obvious markings, and it seems almost incredible that anyone might have imagined that the moon and all other celestial bodies were perfect. And yet that was the prevailing belief until the Renaissance.
Despite the markings, though, there is not one crater that is visible as such without optical aid. Not one! The rays of some of the fresher craters, such as Tycho, are on the edge of detectability, and of course many of the larger "seas" have their origins in large impacts, but barring these borderline properties, one needs some kind of aid to see craters. But even in a lowly pair of binoculars, dozens of craters are simple to see.
Many beginners think of observing the moon when it is full, since that's when most of it is visible, but they quickly learn what experienced observers already know—that it's among the worst times to observe the moon. The problem is that the moon is then so uniformly illuminated that little detail is visible. Neutral density (gray) filters can be used to improve matters somewhat, but they only make lunar observing around full moon less painful. The same effect can be achieved, in steady skies, simply by increasing the magnification.
Incidentally, even though the moon seems blindingly bright through the telescope at these times, it really is a very dark object. On average its surface reflects only about 10 percent of the light hitting it—this is known as its albedo. If you have trouble believing this figure, you can determine for yourself how an object can still appear very bright under those circumstances by going into a dark closet with a sheet of black construction paper and a flashlight. Shining the flashlight on the paper produces a fairly bright disc, even though the paper reflects no more than a few percent of the light hitting it, much like the moon.
The greatest detail can be seen around first or last quarter, when the moon is half illuminated, especially along the terminator, the border between light and dark. There the shadows of crater walls and mountains are long and distinctive, drawing the texture of the moon into sharp relief. One splendid example is the crater Copernicus, among the most prominent of them all. It is near the center, to the selenographic northwest. (Selenography is to the moon what geography is to the earth, and selenographic northwest is to the upper left in a pair of binoculars, just what you would be used to from looking at maps of earth.) It is a large crater, surrounded by a huge system of rays, fresh streaks of moon dust thrown up by recent impacts.
Possibly the brightest and best of the lunar craters is Tycho, near the north lunar pole. It is not especially large, but it is distinguished with the most extensive system of rays on the lunar sphere, on either side of the moon. These rays are still bright by virtue of their newness; in a billion years, these will have faded while the crater itself will still be deep, although it will not be so easy to find.
Another popular crater for lunar examiners is Plato, a broad crater near the south lunar pole. It is somewhat unusually formed—most craters are bowl-shaped, with the larger and newer ones having a central spike, but a few, like Plato, were filled by lava after forming and are flat-bottomed. It is well-known for containing an array of craterlets, which are small craters located within Plato itself. The largest of these craterlets are about 3 or 4 km across, which would not be so hard to see if Plato were near the lunar equator. As it is, they are detectable in a quality 4-inch telescope when the seeing is steady.
Near the center of the moon is a series of three large craters; from north to south, these are Ptolemaeus, Alphonsus, and Arzachel. Just to selenographic west of the last of these is the famous Rupes Recta, the Straight Wall. It's a long crease in the moon, about 150 to 200 km long. It used to be thought to be a sheer cliff, like Half Dome in Yosemite National Park, but in fact the slope is comparatively gentle, about a 10 percent grade from west to east.
Perhaps it makes sense that Copernicus gets a nicer crater than Ptolemaeus, since it was Copernicus that first published a treatment of the sun-centered universe that ushered out the Ptolemaeian earth-centered system that had held sway for a millennium and a half. But who are Alphonsus and Arzachel, and how did they get such large craters?
By way of explaining this, let's note that the first to make a concerted effort to provide a lunar nomenclature was the 17th-century German astronomer Johannes Hevelius. He named most of the large "bodies of water" on the moon, such as Mare Tranquilitatis, the Sea of Tranquility, where Apollo 11 landed in 1969. He laid down a protocol of not using people, dead or alive, for place names.
This protocol was promptly discarded by an Italian astronomer named Giovanni Riccioli, who published the New Almagest in 1651. He decided to go about naming the lunar craters, and he decided to name them after people, typically astronomers and other scientists but also others who promoted science in their own way. In so doing, he started a tradition that has continued to the present day, and so for instance we have a crater named Einstein, near the eastern limb. (Hevelius and Riccioli themselves have small craters near the western limb, at the lunar equator.)
It turns out that Alphonsus X was a 13th-century Castilian monarch. As a political and military man he was no hot stuff, but he was a patron of the sciences, and Riccioli could respect that, so he laid him next to Ptolemaeus (who we know better as Ptolemy). Arzachel is Ibn Ar-zaqala, an Islamic astronomer from the 11th century who lived in Spain. If Riccioli gave us a legacy of personal crater names at least the legacy was a multinational one and not a miasma of classical and Italian names.
You wouldn't consider the OED to be a source of scientific reference knowledge (well, come to think of it, why not?), but it also reveals that the moon is the chief cause of the tides. Now what about those tides? We now know that the sun is about 400 times as distant as the moon, but it is also 25 million times as massive. How could the puny moon, as close as it is, exert more of an influence than the distant but almost incomparably huger sun?
To puzzle this out, we need to understand how the tides are caused. Followers of the tides—surfers, for instance—know that high tide passes about twice a day, and that it coincides with those times when the moon is either as nearly overhead as it gets that day, or else directly on the other side of the earth, as nearly "underfoot" as it gets that day. From the perspective of someone looking down on the earth from far above, the oceans bulge in two places, one pointing directly toward the moon, and one pointing directly away from it.
How is it that the moon can push the ocean away from itself? Isn't this some kind of violation of the supposedly universal law of gravitation? Actually, it's gravity itself that makes this possible. As Isaac Newton formulated it, the force of gravity decreases with the square of the distance, so that the moon pulls on the sun as well as the earth, but because the sun is 400 times more distant, the moon's pull on the sun is about 4002 or 160,000 times weaker than its pull on the earth. This just by the way.

Suppose that the earth were in three pieces—the rocky body that we normally walk on, the body of ocean facing the moon, and the body of ocean facing away from the moon (see Figure 1). The moon is closest to the body of ocean facing it, so that body feels the greatest pull of the moon's gravity. The rocky earth is a bit further away, so it is pulled a little bit less, yielding the high tide on the near side. And the body of ocean facing away from the moon is further still, so it is pulled even less than the rocky body of the earth. What produces the high tide on the far side of the earth, then, is not the moon pushing that water, but the moon pulling the water less than the solid earth. Of course the earth isn't really in three pieces, but the only thing that matters here is the differential application of the earth's gravity, and as far as that's concerned the difference between three pieces and countless trillions is trivial.
In other words, the tides are caused not by the force of gravity itself, but by how that force varies across the width of the earth. As we mentioned above, the force of gravity decreases as the square of the distance between two objects, and calculus—also due to Newton—tells us that the variation in that force, and therefore the tidal strength, decreases as the cube of the distance.
Thus, if the sun were only as massive as the moon, and as far away as it is now, the tidal influence of the sun would be 4003 or 64 million times weaker than the moon's. It is only because the sun is so much more massive than the moon that its influence can be felt at all, but even with its immense size, the moon still has the lion's share of the influence on our tides, in the proportion 64 million to 25 million, or about 5 to 2. The other planets contribute next to nothing to the ocean tides; the largest influence comes from Jupiter's, and with a mass only about 25,000 times that of the moon, its tidal influence is about 0.00003 percent as strong as that of the moon.
People have always considered the sun important, though, and for good reason. In a Peanuts strip, Charlie Brown wonders what the world would be like if the sun were to fail. Lucy answers, "It would be dark." It would indeed, but that is of course only the start of our troubles.
Actually, it would take a little over 8 minutes before we would know anything of this failure, if it happened suddenly enough, for that is how long it takes any information, travelling at the speed of light, to get from the sun to us here on earth. At that point, the sky would become instantly dark, as dark as the night sky is normally—possibly even darker as many lights normally on during the night would still be off. Initially, this might be a boon to amateur astronomers everywhere, but the atmosphere would only retain heat for so long. It would take little time for the catastrophe to overtake nearly all life on earth. Only those organisms that can make a living off of non-solar energy sources—such as some species of bacteria living off of thermal vents in the ocean—would be able to survive for any appreciable period of time.
Given the sun's vast importance to us, it's not surprising that in civilizations in which they were noticed at all, solar eclipses were looked upon almost universally as bad omens. Even today, in our supposedly well-informed world, pregnant women in some areas are urged to stay indoors with the window shades drawn during an eclipse, for fear of damage to the fetus. It's equally unsurprising that a special premium was placed on the ability to predict solar eclipses. We have good evidence that eclipses could be predicted as soon as a few hundred years before Christ, and the early point might be considerably before that. (The story about the ancient Chinese astronomers, Hsi and Ho, being beheaded around 2000 B.C. for failing to properly forecast a solar eclipse is probably apocryphal, though.)
Such predictions, incidentally, could only predict that a solar eclipse would occur on a given day. This only requires precision on the order of the width of the moon, which may seem surprising for a moment, since the splendor of a solar eclipse is in large part due to the exactness with which the lunar disc fits in front of the sun. But consider that the moon, at about 3,475 km across, is significantly smaller than the earth. If the error in a prediction of lunar position is off by the width of the moon—if the moon is off by 3,475 km—then its shadow on the earth will shift by only a little more than that 3,475 km. The earth is about 12,760 km across, so such an error will not usually remove an eclipse altogether, though it will move it somewhere else on the face of the earth, and it might change it from a total eclipse to a partial or annular one (or vice versa).
For 20th-century eclipse chasers, however, who travel thousands of kilometers in search of the ultimate eclipse experience, greater precision is needed. An eclipse is typically total over only a very narrow band on the earth, sometimes as little as a couple of tens of kilometers wide. To predict the path of an eclipse to within a kilometer or so, we need to predict the position of the moon to within about a second of arc—that is, 1/3,600 of a degree!
You might think that predicting the position of the moon would be relatively easy. After all, it revolves around the earth, and we don't need to deal with retrograde motion the way that we must do for the other planets. But in point of fact, the moon is one of the hardest objects to construct a theory for. Such a lunar theory begins with an ellipse, but must then account for a series of perturbations resulting from the gravitational pull of all the various other objects in the solar system. To predict the position of the moon to within even a few minutes of arc—say, a tenth of a degree—one requires a lunar theory with about 10 perturbation terms. Our old friend Newton was said to have complained that the problem of the moon's motion was the only one that made his head ache.
We close with a curious optical illusion, popularly called the moon illusion. Simply put, it is the perception that the moon is larger when it is at the horizon. It clearly cannot be actually larger, for while it is at the horizon for you, it is high in the sky for some other observers, and the same moon cannot be two different sizes. The moon is also not any closer when it is at the horizon; in fact, because you are looking across half of the earth's width, the moon is actually some 6,380 km further away at those times than when it is high overhead. But because the total distance is actually some 384,000 km, such a difference is difficult to notice. At that distance, the moon spans some 30 minutes of arc, or half a degree.
In spite of these rationalizations, the illusion is surprisingly persistent. The Greeks believed the illusion was due to the observer's subconscious comparison with earthly features on the horizon. The moon dwarfs distant trees and hills; the argument is that those same size cues are absent when the moon is high overhead, and our minds do not "expand" the moon's size in compensation. But the moon illusion persists even at sea, when there is a lack of features to compare it to.
Another explanation frequently offered in the past is that the moon appears larger at the horizon because of atmospheric distortion. It is true that the earth's atmosphere refracts light and that it can affect the shapes and sizes of distant objects. But atmospheric distortion actually compresses images in the vertical direction, leaving them unaffected in the horizontal direction. As a result, the moon (and the sun, for that matter) would appear smaller—flattened, squatter, but no wider.
The modern view is that there are a number of explanations that together contribute to the moon illusion, but predominant among them is the mind's expectation that the moon is actually considerably further away when it is at the horizon. The common image of the sky is that of a blue dome enclosing us and touching the earth at the horizon. But this dome appears closer to us directly overhead than it does at the horizon. For instance, clouds appear to grow in size when they approach and decrease in size when they leave. Observations like these generate the impression that the dome is flattened. (See Figure 2.)
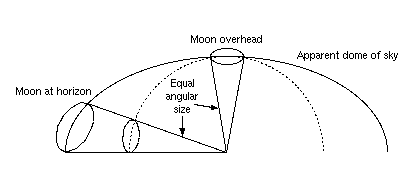
If the moon were substantially closer when overhead than at the horizon, and in either case appeared the same size, then it would obviously have to be larger at the horizon, in order to make up for the fact that it was then further away. It makes no difference at all that it isn't that much further away; the expectation that it is is sufficient to create the illusion.
You might find it entertaining to investigate the various factors leading up to the illusion yourself. Try looking at the moon through a paper towel roll—this time without any inexpensive Edmund Scientific optics in it—and see if the illusion persists. Some sources suggest that if you do so and keep your other eye open, you'll see two views of the moon, one exhibiting the illusion and the other one not! I can't reproduce this result, but if you give it a try, I'd love to hear what you see. Send me an e-mail at <brian.y.tung@gmail.com>, and if I get enough responses, I'll summarize them in a future column. In the meantime, clear and steady skies, and happy observing!
Copyright (c) 1999 Brian Tung