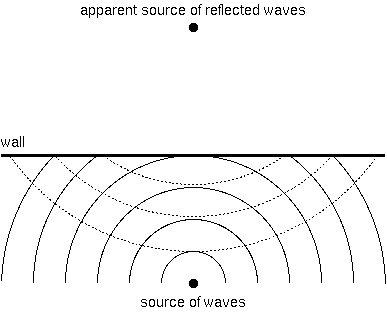
Figure 1. How water or sound waves reflect off an obstacle.
As we lay huddled together under the tent, which leaked considerably about the sides, with our baggage at our feet, we listened to some of the grandest thunder which I ever heard, —rapid peals, round and plump, bang, bang, bang in succession, like artillery from some fortress in the sky; and the lightning was proportionally brilliant. The Indian said, 'It must be good powder.' All for the benefit of the moose and us, echoing far over the concealed lakes.
—Henry David Thoreau, The Maine Woods
EVERY NOW and then, someone asks me how I decide what I'm going to write about in these essays. I wish I knew, so I could mine it more consistently. On second thought, though, I probably have to leave it to random chance, at least some of the time. There's only so much you can do to force out a topic on a regular, or even semi-regular, basis.
For instance, I had decided a while ago to compose an essay on how the planets, and in particular Jupiter, affect the orbits of comets and unmanned explorers alike as they wander around the solar system. I had even worked out in my mind the general organization of the essay.
But then, I was in San Diego on business, and I was walking back from my car to the hotel, talking with my wife about something or other, when I realized I could hear my own words echoing indistinctly back to me. I remarked on how strong the echo was, and then I forgot about it.
The next day, I was loading up the car before driving back home, and this time, without intervening conversation and extraneous noises, I could hear the shuffling of my feet very distinctly indeed, echoing off the hotel and bouncing back to me. The hotel walls were far enough away that I could expect to hear a separate sound, but it seemed to me that it was much louder than I had any right to expect.
It would be one thing if the hotel were curved, and I were standing at the center of curvature. If you're in a circular room, all the sound waves that you emit will come bouncing right back to you. Even if only part of the circle is there, enough sound will still come back to represent a noticeable echo. But the hotel walls were not curved at all.
I stood there a while, looking at the hotel, trying to puzzle it out, when it suddenly came to me. I understood just why the echo was so strong. And what's more, a quick train of thought led me to how we measure the distance to the Moon with astonishing precision. I simply had to write an essay about it.
So here we are.
The notion of sound as a wave in air is part of human history. Early humans had no idea of sound beyond something that their ears could hear. Loud sounds could be muffled, either by covering the ears, or by covering up the object making the sound. This made sense. Clearly, by covering up the object, most of the sound was trapped, so you couldn't hear it as distinctly; by covering up your ears, most of the sound was kept out of your ears, and again, you couldn't hear it as distinctly. None of this requires any idea of sound as a wave travelling in air.
Even early on, however, there must have been some twinkling of an idea that sound and waves were related. On large drums, the skin of the drum can be seen quite noticeably vibrating, and if the skin is not drawn too tight, that vibration is slow enough to be seen moving back and forth (and the drum produces a very loud and low sound). It looks just like the shape and motion of waves on water, only much faster. This relationship was drawn more clearly by Pythagoras in the sixth century B.C., in his investigations into musical strings and the pitches they play, as described in my last essay, albeit in a different context.
If you drop a stone into a pool of water, we all know what happens: a set of circular waves spread out from where the stone goes in. And if those waves encounter an obstacle—a straight wall, say—the waves bounce back or reflect, much as a ball would. For a while, the original waves and the reflected ones criss-cross in an entertaining way, but after that, all you can see are the reflected waves, which look as though they came from a spot behind the wall.
Aristotle (384–322 B.C.) was clever enough to see a parallel between the way waves propagate on the surface of the pool and the way sound propagates in air, and he proposed that they were the same, in a treatise entitled "On Sound and on Hearing." The Greek engineer Vitruv (c. 90–20 B.C.) countered that water waves propagate only on the surface of the water, whereas sound propagates throughout the atmosphere—not just on its surface (wherever that might be).
All the same, if we latch onto the notion of sound being a wave, is there anything in our experience that resembles the action of water waves bouncing off a wall? Aristotle arived at one obvious answer—the echo. He even compared it to a ball bouncing off a wall:
An echo emerges when air, that is considered a body in relation to the space where it is contained, cannot further move due to the boundaries of this space and is thrown back like a ball by the walls of this space.
In both water and sound echoes, the waves emanate from their source and reflect off the wall in a characteristic pattern, as shown in Figure 1, below. The original waves are shown as solid curved lines, and the reflected ones as dashed ones.

Note that the reflected waves look just like the original ones, except that they appear to come from a point behind the wall. That's why echoes work. The caveat is that the sound appears to come from a distance twice as far away as the wall. If you try an echo against a cliff wall a mile away, the echo will seem to come from two miles away, and everyone knows you have to shout pretty loudly to be heard from two miles away. That's why I was initially so puzzled that the echo from the hotel seemed so distinct that I could even hear my feet shuffling against the pebbles in the parking lot.
You might well ask how we know that the wave bounces off the wall this way. A wave is not a localized phenomenon—if you look at a wavefront, you cannot say that the wave is at any particular point in space. It is everywhere along the wavefront at once. It's not at all obvious how the wave should reflect from the wall. It certainly doesn't seem like throwing a ball against a wall. If we were to throw a hula hoop against the wall, for instance, it might make a loud clatter, but it wouldn't look like Figure 1. Why not?
The difference is that the wave, although it appears to be a single connected thing, isn't actually. In the case of water waves, it's the collective motion of lots of water molecules; in the case of sound waves, it's the collective motion of lots of air molecules. In neither case do the molecules themselves actually move outward from the source along the wavefront. Instead, one region of molecules moves back and forth, and in so doing, they knock the next region of molecules to move back and forth, and then the next region, and so on. (That's why you can't have sound in space—because there aren't enough molecules to knock into each other to transmit a wave motion.) Only when you look at the molecules from a wide perspective do you see the moving wavefront.
Suppose we follow the jostling motion as it's transmitted outward, region by region, by the molecules. The jostling region would start at the source of the waves, and it would move outward at a certain rate. We could then view a wavefront as being composed of lots of little regions of jostling motion. The little regions aren't connected together in any rigid way, but all things remaining equal in the different directions, we would expect them to spread outward at the same rate in each direction, creating a circular wavefront (or spherical, in the case of sound waves), as in Figure 2.
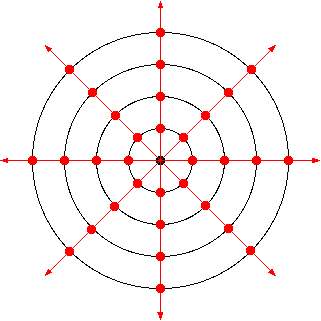
This double interpretation of waves as either existing all at once, or as a collection of wave regions, or particles, is quite common in science—common enough that there is a specific term for it: we say that the wave interpretation and particle interpretation are duals of each other. Such duals often have interlocking properties. Note that at any point in Figure 2, the path traversed by a wave particle is perpendicular to the advancing wavefront. That means that if you know either the path of the wave particles or the shape of the wavefront, you can determine the other.
(The relationship goes even deeper; the two are interchangeable. Suppose you could engineer a situation in which a straight wavefront travelled around a central point, as though you were swinging a stick around you in a circle. The wave particles would then be moving in circular paths around that central point. It would look exactly like Figure 2, except that the wavefront and the wave particle paths would have switched places.)
Even though the two interpretations are equivalent, there's an advantage of looking at waves as a collection of wave particles is that the particles can be made as small as you like. When they strike the wall, they can be viewed as bouncing off it just as a ball would. Each wave particle reflects off the wall in accordance with the law of reflection (see "Diffraction" for more about this). And if we connect the dots on the wave particles after they reflect off the wall, we get exactly the shape we see in Figure 1—a further justification of our dual interpretation of the wave.
Looking at waves in a particle way also makes it easier to see what happens when the wave reflects off more than one wall. We can look at isolated wave regions and trace their path in accordance with the law of reflection. Suppose that we have two walls that meet at a right angle. As you can tell from Figure 3, no matter how you throw a ball at such a pair of walls, it will always bounce back in the same direction from which it came.
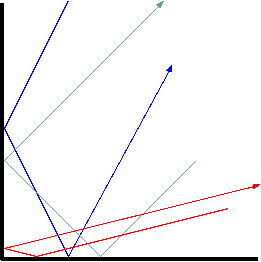
That would also happen to water waves. If a straight wavefront in water were to encounter the two walls, it would reflect off them and return in exactly the same orientation and opposite direction that it came.
It's a little different with sound waves, but only a little. The only difference is that, as Vitruv pointed out, sound waves travel in three dimensions, while water waves travel in two. The only thing we need to do is add a third wall, at right angles to the other two, just as two walls meet a ceiling. Then waves in even three dimensions will go back in the same direction they came.
Such "triple corners" are obviously very common on the insides of buildings, but generally speaking the rooms are so small, and the speed of sound so fast, that you can't hear a separate echo. You hear it right on top of the original sound and it just sounds like one sound. On the outside of buildings, where you can get far enough away, triple corners are less common, and all you get is the relatively weak echo that comes from a straight exterior wall.
But the hotel I was staying at, I eventually realized, had lots of triple corners all over the place. That rooms were arranged in a slanted manner, like the slots in many parking lots, so instead of being one flat wall, the exterior was composed of numerous wall segments meeting at right angles. Then, too, each of the rooms had a balcony, which naturally jutted out from each of the concave joints of the wall segments. Under each of the balconies, therefore, was a triple corner that reflect sound right back to me.
What I heard, then, was not one echo. What I heard was one echo for each balcony, all reflecting the sound back to me. Small wonder that the echo was so noticeable that I could hear the echo of dirt scrunching under my feet—could hear it better than I could hear it directly, in fact.
These triple corners will work with other waves than just sound or water waves. They also work with light, and in this context they are known as "triple mirrors" or "retroreflectors." One common application of the triple mirror is the red reflector often placed on the rears of bicycles. They emit no light of their own, but when a car headlight shines on them, they reflect that light back in whichever direction it came. There is enough natural spread so that the driver of the car can always see the reflected light, even though he or she is not directly behind the headlight lamps.
They have more far out applications as well. In the late 1960s and early 1970s, the U.S. and U.S.S.R. were engaged at the height of the space race. Both space programs landed spacecraft on the Moon (although only the U.S. landed manned spacecraft). Along with the usual public relations boon, both programs also installed retroreflectors on the surface.
Obviously, this wasn't just so that we could make sure the Moon was still there. If you point a laser beam at one of the retroflectors, the three mirrors will reflect that light directly back toward the source, where it can be picked up. In particular, the time it takes for light to travel from the Earth to the Moon, and then back, can be timed to great precision, even back in the 1970s; the figures were accurate to about a nanosecond. Since we know the speed of light, we can translate those times into distances, with errors on the order of tens of centimeters—perhaps a foot or so.
At the time, the speed of light in a vacuum wasn't known exactly. (In the early 1980s, it was defined exactly to be 299,792,458 meters per second, so that the length of the meter was defined by both this speed and by the length of the second.) As a result, the distance to the Moon wasn't known with utmost accuracy. Even so, however, we knew how the round trip time changed as the weeks and months passed, and this could be translated into changes in the Earth-Moon distance.
In case this isn't clear, suppose that we measured the round trip time at some moment to be exactly 2.56 seconds. If we only knew the speed of light to a precision of plus/minus 1 meter per second, then the Earth-Moon distance could only be known to a precision of plus/minus half of 1.28 meters. (That's the half of 2.56 seconds times 1 meter per second.) But if a little while later that same round trip time was measured to be 2.56 seconds plus 2 nanoseconds, we know that the Earth-Moon distance must have increased by whatever distance light travels in 2 nanoseconds, which is about 60 centimeters—even if we don't know what the actual distance is.
The reason this is useful is that although the Moon is commonly said to orbit the Earth, that orbit is not perfectly circular, or even perfectly elliptical. (See "Music of the Ellipses.") Superimposed on even the elliptical motion are countless irregularities. Studying these irregularities can reveal long-term trends for the Moon that would otherwise go undetected.
One exciting possibility was found in the 1970s. After dozens of known periodic variations in the Earth-Moon distances had been explained and accounted for, one oscillation remained, with an amplitude of several tens of centimeters. Such oscillations are not uncommon in the solar system; sometimes, they are caused by asymmetries, either in the orbit or in the bodies themselves. (For instance, the Moon seems to be slightly lop-sided, with the denser "end" facing us.) But the period of this particular oscillation didn't seem to fit any of these explanations.
Another possibility is that the Moon was struck, at some point in time, by a sufficiently massive object to start it swinging back and forth. As it so happens, there was a record, back in 1178, of an impact observed on the Moon by a group of Canterbury monks. The observations were recorded by a monk named Gervase, who was then chronicler at Canterbury. Could it possibly be responsible for the oscillation detected by a curious combination of ancient and modern science—triple mirrors and laser beams—almost eight centuries later?
Preliminary back-of-the-envelope calculations suggested that it was a definite possibility. Although uncertainties were significant, the results were consistent with an impact origin for the oscillations. Adding to the excitement was the identification of a candidate crater, called Giordano Bruno, evidently the freshest of its size anywhere on the Moon. In 1976, Jack Hartung, then a geologist at the State University of New York, suggested that Gervase's passage describes the creation of Giordano Bruno, and for many years, it was popularly believed that the Canterbury monks really had observed an impact on the Moon—an event that should happen perhaps several times in a million years. This account even appears in Carl Sagan's widely acclaimed television series, Cosmos.
Alas, it now appears that it was instead a trick of the eye. First of all, no collision was reported by observers in countries such as China, which had a long history of astronomical observations, and where astronomy was approaching its height. It was difficult to believe that such a cataclysmic event, which had longer-term effects (the monks reported that the Moon took on a charred appearance), could have gone undetected by everyone else.
Secondly, and more damning, was a calculation based on the size of Giordano Bruno, and furthermore of any impact that would be large enough to be visible to the unaided eye. Paul Withers, a graduate student in planetary science at the University of Arizona, wrote in the April 2001 issue of Meteoritics that an impact explosive enough to have created the 22-km crater would have ejected about 10 million tons of material. That is enough, Withers calculated, to have produced meteor storms for a week. Yet not one report was made of such storms—not from Europe, not from China, not from anywhere. Withers' analysis of the laser measurements suggested that the fluctuations in the lunar distance were indeed real, but were caused instead by fluid motions in the core of the Moon. (Withers has since gone on to receive his Ph.D. in planetary science.)
Putting the nail in the coffin, the Clementine lunar explorer showed that while Giordano Bruno is in fact relatively young, it is only relatively so, and must be far in excess of 800 years old. So what did the Canterbury monks see? Recently, it's been proposed that what they saw was nothing more than atmospheric effects on the Moon, which was then in its crescent phase and would have been seen close to the horizon—exactly when atmospheric effects would play the largest role.
It's a shame, because it's such an outstanding story, and I always find myself pulling for people in a far-gone era to make scientifically significant observations. But one can't wish scientific significance into an observation that lacks it.
One final comment about the lack of a meteor storm following the putative impact on the Moon. It isn't just speculation; one can show, fairly rigorously, that eject from such an impact eventually has to either land on the Earth as a meteor shower or escape the Earth-Moon system altogether, and there's no way to get it all to do one or all to do the other. It has to go both ways.
Such considerations also became involved in trying to figure out how the Moon formed in the first place. Currently, the best theory of the Moon's creation has it being formed from the ring of ejecta shot out when a Mars-sized planetoid struck the primitive Earth early in the history of the solar system.
There are now simulation studies to back this theory up, but one of the problems encountered in validating the theory was coming up with the initial conditions of the impact (velocity, direction, how far off center the impact was, and so forth) that would result in just one Moon. Either too much material would spiral in and out, or multiple Moons would be created, or something. It turned out to be non-trivial to set up the right initial conditions—not so tricky that the theory was judged implausible, but tricky all the same.
Fortunately, there are a broad class of initial conditions that give us our current situation, a single Moon orbiting us at a distance of 385,000 km.
Copyright (c) 2005 Brian Tung