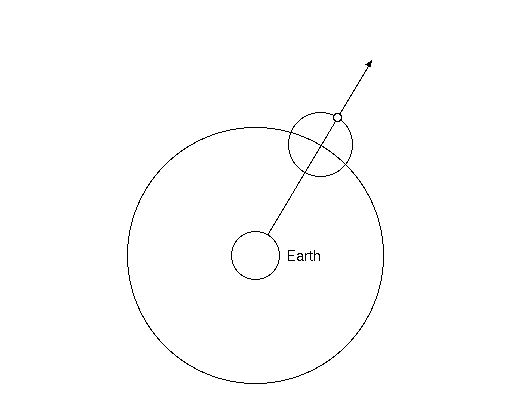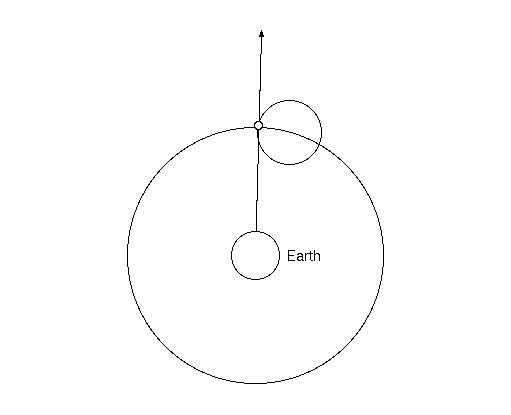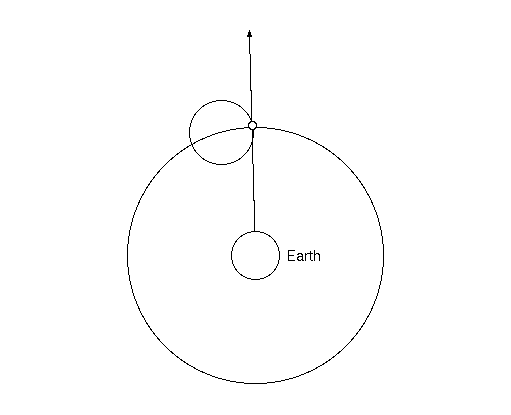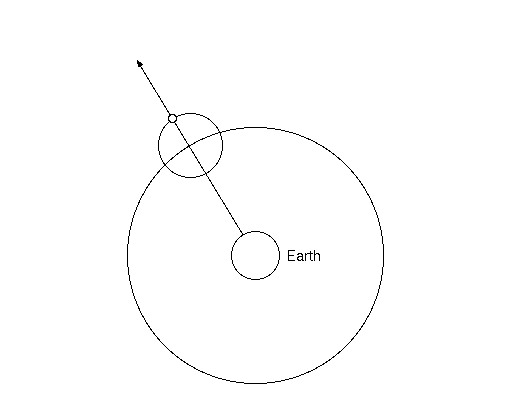
Figure 1. How an epicycle can explain retrograde motion.
Mankind is not a circle with a single center but an ellipse with two focal points of which facts are one and ideas are the other.
—Victor Hugo, Les Misérables
A SEMI-RECENT survey [1] showed that about a quarter of American adults believe that the Sun goes around the Earth. You can imagine the uproar that rose up in educational institutions around the country. (Actually, it was pretty subdued, and if you were of a cynical bent, you could draw some pretty depressing conclusions about what higher education thinks of the American mandatory educational system. But let's not get into that.) How is it possible that so many Americans could believe such a thing?
Well, they believe it for the same reason that the ancient Greeks and everyone else up to about the 16th century believed it. All you have to do is look up, and if you have the common sense God granted the garden snail, it is plain to see that the Sun goes around the Earth. After all, astronomers claim the Moon goes around the Earth, and no one laughs at them for that.
Granted, appearances were not all that mattered to the Greeks. They had their theory, too. Aristotelian physics held that the Earth was all that was base and ignoble, and it therefore sank to the very center of the universe. The celestial objects, however—everything up in the sky—were good and noble, and therefore light and airy, and they all travelled in great circular arcs around the lowly center, maintaining a cordial distance at all times.
However, the Greeks were no dummies. If it had been clear from observation that it was the Earth that went about the Sun, and not the other way around, they would have adapted that into their theories. It wasn't their fault that appearances were so deceiving that they arrived at the wrong conclusions. They made a perfectly reasonable stab at the truth.
So let's take a look at how that reasonable stab at the truth became unreasonable fiction.
Anyone who pays attention to the night sky for any significant period of time soon notices that it moves with surprising regularity. For the most part, stars rise in the east and set in the west, like the Sun, and those that don't, move in perfectly reasonable circles around the north pole star, Polaris.
There are a couple of thousand stars visible to the unaided eye on any given night, so it becomes something of a hassle to have to keep track of them individually. To simplify things, people picked up the trick of grouping them into constellations. Instead of having to remember a couple of thousand stars, they only needed to memorize a few dozen constellations. If you observe the constellations over the period of a year or two, you also notice that the same constellations don't rise at the same time every night, but neither do they appear willy-nilly, wherever and whenever they want. There is a set order to them, and they follow that order, year in and year out. In other words, although the stars arc across the sky each night, they don't move with respect to one another. It's as though they were stuck onto a huge black dome, and the dome moved around the Earth as a whole. In fact, astronomers from ancient times have occasionally called the stars, specifically, the fixed stars.
Against these law-abiding points of light in the heavens are set a few bodies that do not follow these simple rules. These bodies rise and set once a day, to be sure, but they do not move as though they were stuck onto the dome of the sky. Rather, they move with respect to the stars, and they can be seen wandering from constellation to constellation, over a period of weeks and months (and in the case of the Moon, from day to day). The Greeks called these bodies "planetes," from their word for wander, and that's where we get our word "planet." To the Greeks, anything that wandered from place to place was a planet, so the list of planets, in toto, read as follows:
Sun
Moon
Mercury
Venus
Mars
Jupiter
Saturn
The Sun and Moon are, of course, no longer thought of as planets. Of the remaining five, Mercury and Venus orbit the Sun closer than does the Earth—although the ancient Greeks didn't know that—and therefore never appear very far from it. In fact, for much of the time, either planet is too close to the Sun to be seen without safety precautions. The rest of the time, the planet is either west of the Sun, and therefore only appears in the morning, before sunrise, or it's east of the Sun, and therefore only appears in the evening, after sunset.
The Greeks, in fact, had two different names for Venus. They called its morning apparition, or appearance, Phosphoros (Greek for light-bringer, which the Romans transformed into Lucifer), and they called its evening apparition, Hesperos (Greek for west, which the Romans transformed into Vesper). It took the Greek philosopher and mathematician Pythagoras (c. 560–480 B.C.) to realize they were one and the same planet, although he may have gotten the idea from the Babylonians.
If we concentrate our attention on the planets Mars, Jupiter, and Saturn, we notice that not only do they not stay in place with respect to the well-behaved stars, but they don't even follow nice, circular paths across the sky. If we plot their positions against the stars, we find instead that their paths are uneven. Generally, they move west to east, but sometimes they move east to west, and occasionally, they make a wide loop, up and over, as if they couldn't decide which way they wanted to go. When a planet moves in the "wrong" direction, that is called retrograde motion (as opposed to direct, which is motion in the "right" direction).
This troubled the Pythagoreans. They felt that the circle was the acme of perfection as far as shapes were concerned, and since the planets were just as much celestial objects as the stars, they should all be moving in circles. However, for all that they were absorbed in the world of the ideals, the Pythagoreans couldn't go against appearances that much. Certainly one could not describe the motion of Mars, say, with just one circle. A follower of Pythagoras, the Greek philosopher Plato (c. 427–347 B.C.), spent a good deal of time himself on reconciling planetary motions to circles, without much success. So he posed the following open question: Could one describe it with a combination of circles?
The first really explicit attempt at answering Plato's question in the affirmative was made by the Greek philosopher, astronomer, and mathematician Eudoxus of Cnidus (c. 400–347 B.C.). His solution used spheres, which were all right by the Pythagoreans, since a sphere is nothing more than the perfection of the circle raised to the third dimension. Eudoxus proposed that the weird loop-the-loop motion of Mars could be explained if it were on the equator of a rotating sphere. But not a freely rotating sphere. No, Eudoxus added a second sphere, set at an angle to the first, and to which the first sphere was attached.
To explain the complex motion of Mars, Eudoxus had the second sphere rotate in roughly the opposite direction to the first, and at the same speed. And since they rotated at the same speed, when the first sphere completed one rotation, the second sphere did too, so that Mars would end up back in the same place. But in between, because the spheres were set at an angle to one another, Mars would not remain stationary, but would instead trace out a figure-8 like shape. If you superimposed this figure-8 on the otherwise smooth west-to-east motion of the planets, Eudoxus suggested, you would get a planet that usually moved west to east, but that moved the other way from time to time, describing loops that went first up, then down, then up again, and so on. Because the figure-8 resembled the path of a horse on a fetter, this mechanism was called the "hippopedes," which is Greek for horse-fetter.
The hippopedes explained, in broad terms, the strange motion of some of the planets, and it had the advantage of involving only the perfect shapes of spheres and circles. But it failed in important ways, too. It didn't explain why the seasons had different lengths—that is, why summer was a few days longer than winter. It didn't match the actual orbits of Mars, Jupiter, and Saturn, even to the limited precision of the observations then available, and it didn't come close to explaining the motions of Mercury and Venus. (However, it wasn't a total loss. If we interpret the motions of the two spheres as the Earth orbiting the Sun in one case, and the Earth rotating on its axis in the other, then we get a very good explanation of the figure-8 shape of the analemma, the curious sigil that appears in the South Pacific on some globes. But that's a matter for another essay.)
A partial step forward was made by the greatest astronomer of antiquity, Hipparchus of Rhodes (c. 190–120 B.C.). Hipparchus seems to have taken as his starting point a work on eccentrics and equants by the Greek geometer, Apollonius of Perga (c. 262–190 B.C.). He then extended and applied it to the question of lunar and solar motion.
The motion of the Moon was particularly difficult to explain. On the whole it goes around the Earth about once a month (hence its name, as described in "The Moon"). However, it doesn't move uniformly, as you'd expect. Instead, it constantly speeds up and slows down, an effect called the lunar anomaly. This is a result of its elliptical orbit and gravitational perturbations from the Sun, the Earth's equatorial bulge, and the other planets. However, Hipparchus wasn't aware of the causes of the anomaly, and in any case he was only interested in a mathematical model of the Moon's behavior. He didn't care about why the Moon went every which way—he only wanted to explain how it moved.
Here was the model devised by Hipparchus: The Moon was indeed carried around the Earth by a circular orbit. But the Moon lay not on the orbit itself, but rather at the edge of a sort of wheel, or epicycle. It was the center of the epicycle that went around the Earth in uniform circular motion, while the Moon in turn went around the center of the epicycle. When the Moon was moving in the same direction as the epicycle, it appeared to speed up; when it was moving in the opposite direction, it would appear to slow down.
Hipparchus went on to describe the motion of the Sun in terms of epicycles also, and this model worked reasonably well. However, having the sort of integrity that he did, Hipparchus had to admit to himself (and to others) that his lunar model, although it agreed with actual lunar observations when it came to the general effects of the anomaly, it did not agree when it came to the finer aspects.
Although Hipparchus was the greatest astronomer of antiquity, very little of his actual writing survives, unfortunately. The little we do have is a three-volume review of two other Greek works, and only in the second half of the set do we get any of Hipparchus's own theories. Fortunately, much of that theory was not lost yet at the time of the Greek astronomer and geographer, Ptolemy (c. 85–165, and no relation to the succession of Egyptian kings). Ptolemy collected the various ideas of Hipparchus, and synthesized them into a coherent whole, which he called Syntaxis Mathematica, which is Greek for "Mathematical Collection." Almost immediately, however, that title was enhanced by the appellation, "Megiste," meaning "greatest." When the Syntaxis was translated into Arabic, they took heed of that honorific, and we now know the work best by its Arabic name, Almagest.
It used to be thought that Hipparchus was the innovator, and Ptolemy only the poor, beknighted compiler that followed everything that Hipparchus said. For example, one of the other sections of the Almagest is a star catalogue of about 1,000 stars. It contains, interestingly, a number of stars whose positions only make sense if they were observed during Hipparchus's time, not Ptolemy's.
However, in more recent times, it has become evident that Ptolemy was more than just a compiler, and indeed made important contributions to Greek astronomy. For example, Ptolemy made the corrections to the epicycle model of Hipparchus in order to account for discrepancies in the Moon's motion. He also extended the epicycle model to the planets, which Hipparchus did not attempt. Ptolemy showed that if the epicycle turned roughly once a year, and were the appropriate size, the resulting apparent motion would show the correct retrograde motion. (See Figure 1.)

Even if he drew a significant amount of this work from Hipparchus, at the very least he can be credited with doing for astronomy what Euclid did for geometry with Elements—that is, putting everything in order. In fact, Ptolemy put everything in such good order, and predicted the motions of the planets to such a high accuracy, that his work was not surpassed for over a thousand years.
That is not to say it was without its problems. For example, the epicycle model for the Moon that Ptolemy adapted from Hipparchus unfortunately predicted that the Moon should be half as far from the Earth at some times than it was at others. If that were really the case, the Moon should sometimes appear twice as wide as it does at other times. Very plainly, that was not the case, but it doesn't appear to have bothered Ptolemy overmuch, since he, like Hipparchus, was only interested in a mathematical model of the motions of the planets.
That thinking also dominated most of Europe for the next 1,000 years or so. One of the trademarks of the Dark Ages was a marked refusal to do anything but refine the old classics. It is clear in hindsight that there was something fundamentally wrong with the Ptolemaic model, but what better model was there? There was little inclination for anyone to do the kind of tedious, painstaking accurate observations that were required to propose an alternative.
Even when things changed, they didn't change much. The Polish cleric Nicolas Copernicus (1473–1543), near the end of his life, published De Revolutionibus, in which he described his alternative: that the Earth, along with all of the other planets (besides the Moon and the Sun), revolved around the Sun. But even then, Copernicus wasn't spurred on by improved observations of the planets. Those wouldn't come around until the time of the Danish astronomer Tycho Brahe (1546–1601) half a century later. Instead, Copernicus was motivated by the fundamental ad hockery of the Ptolemaic system. It involved a large number of parameters, each of which could be determined by observation alone, and weren't tied to each other in any systematic way. It was his goal to simplify the foundations of celestial mechanics.
There is a persistent myth that in proposing his solution, Copernicus somehow cut the Gordian knot of celestial mechanics that Ptolemy had left tied, that he made computations orders of magnitude easier than they had been before. Actually, computations based on the Copernican model were just as involved as they had been before. Like the Ptolemaic model, the Copernican model used circular orbits, so it retained much of the complicated machinery of the Ptolemaic model. However, what was simpler were the underlying relationships. All the various parameters from the Ptolemaic system was reduced to the tilt of the Earth's axis, its rotation of the Earth on that axis, and its revolution around the Sun (along with the other planets). Everything else could essentially be determined from these three basic factors.
Also, Copernicus wasn't the first to suggest that the Earth went around the Sun. The Greek astronomer Aristarchus (c. 310–230 B.C.) also proposed this idea (see "Double Vision"), as did the German cardinal and philosopher, Nicholas of Cusa (1401–1464). However, Copernicus was the first to set down this model in full, mathematical detail. In his first draft, Copernicus credited Aristarchus in his preface, but in the final version, either he or his printer suppressed the reference—quite likely the latter, in my opinion. After Copernicus's death, the printer was the sole party remaining as a target for persecution. Eager to avoid being singled out, he added a notice to Copernicus's book, that the work was not intended to assert celestial fact, but only to facilitate computation.
Which brings me to the hero of this story. The German astronomer and astrologer Johannes Kepler (1571–1630) was a thoroughgoing Copernican. He was convinced that the Copernican or heliocentric (meaning "Sun-centered") model was celestial fact, rather than just computational facilitator. He was something of a mystic, and he spent much of his life trying (and failing) to demonstrate that the arrangement of the solar system was based on the five regular Platonic solids, which needn't bother us here.
Kepler was also a staunch Protestant, which more than once got him in trouble with the local authorities and forced out of his home. It was during one of these forced evacuations that Tycho Brahe invited Kepler to join him at Uraniborg, Tycho's island observatory. Tycho (who like Galileo is best known by his first name) was a nobleman, with a patron to boot, which meant that he could observe in peace. He was also known as the best visual astronomer around. After more than a millennium, he was the first astronomer to surpass the accuracy of Ptolemy's star catalogue in the Almagest. Whereas Ptolemy's star positions were accurate to about 10 arcminutes, Tycho's were accurate to 1 arcminute, the width of a basketball as seen from a kilometer away. All this without the use of a telescope—that instrument would not be used for astronomical purposes for another decade. Tycho's offer appealed to Kepler, so at the beginning of 1600, he accepted.
As it happened, though, Tycho was long past his best days as an observer. His observing prowess had made him famous, and he was more interested now in entertaining barons than in collaborating with the younger Kepler. It is unclear whether Tycho viewed Kepler as a competitor, but getting observational data out of him proved too difficult for Kepler. When Tycho died the following year following a bout of excess drinking, Kepler mourned but lost no time. Tycho's heirs had no intellectual interest in the reams of data, and they were anxious to sell them as quickly as possible. Kepler had to snap them up quickly before they were lost forever.
Kepler immediately set to work on using the data to prove the validity of the Copernican model. It was not easy work. If the solar system were geocentric (that is, "Earth-centered"), the Earth would be stationary. The apparent paths of the planets would then be due to the actual motions of those planets, and nothing else. But if the Earth were merely one of the planets revolving around the Sun, Tycho's observations were then made from a moving platform. The apparent paths of the planets would be a combination of the actual motion of those planets, plus the motion of the Earth. Worse yet, before the development of astronomical telescopes, there was no good way to tell how close a planet was. Essentially, Kepler was trying to formulate a three-dimensional model from contaminated two-dimensional data.
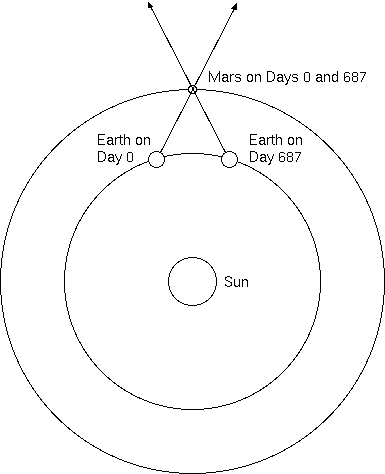
Fortunately, he was Kepler. He realized that although the planets moved from moment to moment, their orbits didn't. If the Earth was in one place at a given time, then it would return to that spot one year later. The same went for the other planets. Mars revolves around the Sun in one Martian year, a little less than 687 days. That meant that if Mars were in one place on a given day, it would again be in that place a little less than 687 days later.
But, and this was the key to the whole enterprise, the Earth would also have moved around the Sun in those 687 days. A Martian year is about 43 days less than two Earth years. That meant the Earth would be about 43 days behind in its orbit at a time when Mars had returned to its original spot. Kepler could then use simple triangulation to determine the true position of Mars in three-dimensional space. (See Figure 2.)
After some months of furious scribbling, Kepler came up with the circular parameters for Mars that seemed to match up with most of Tycho's observations reasonably well—to 2 arcminutes. Tycho's observations were generally accurate to 1 arcminute, but Kepler was willing to overlook that. Alas, two of the observations were off from predictions by as much as 8 arcminutes. That is about one-fourth of the width of the full Moon and 8 times the error in Tycho's observations. As much as he wanted to verify the Copernican model, Kepler could not see his way to ignoring this discrepancy. Tycho's observations were simply too good.
It was at this moment that Kepler took his greatest leap, and abandoned the circle. It meant that the Copernican model was not correct beyond its broadest terms, but Kepler meant to salvage what he saw as its distinguishing feature: heliocentrism. He tried a number of different shapes—ovals of various proportions, egg-like shapes, anything that would fit Tycho's data. Computing three-dimensional positions took pages and pages of tedious computation. In his 1609 Astronomia Nova ("New Astronomy"), he describes not only his results but his efforts as well, taking the reader through even erroneous attempts. "If you are wearied by this tedious procedure," he wrote, "take pity on me who carried out at least seventy trials." He went through so many calculations that he apparently made an error when he first tried the proper shape and rejected it out of hand. According to Kepler, it wasn't until later that he tried the formula again, in a different form, that he performed the computations correctly and found, to his astonishment and delight, that the predictions matched Tycho's observations.
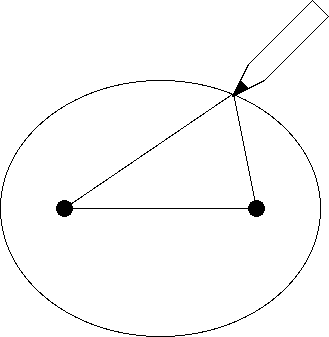
Kepler's solution was an ellipse—a sort of stretched-out circle. In fact, one of the less useful ways to characterize an ellipse is to say that it is a circle with its aspect ratio changed. Here's another way to characterize it: If you have two points, F1 and F2, called foci (singular, focus), and a distance d, then the ellipse is defined as the set of points P such that F1P + F2P is equal to d.
This leads to one simple way to draw an ellipse. If you hammer two nails into a wooden board, and loop a loose string loop around them, you can draw an ellipse by inserting a pencil inside the loop and drawing an oval around the nails, taking care to keep the string taut at all times. (See Figure 3.)
Kepler discovered that the orbit of Mars was perfectly described as an ellipse. What's more, he also discovered that the Sun was not at the center of the ellipse. Instead, it was off-center, at one of the foci (one of the nails, in other words). Actually, this was no surprise to Kepler. It was well-known that the planets were closer to the Sun at certain times than it was at others. Copernicus modelled this by placing the Sun off-center of his orbits, too, and that's what Kepler tried first. However, because Copernicus used circular orbits, he couldn't match the observations nearly as well as Kepler did with his elliptical ones. Kepler's first law of planetary motion is simply this:
Planets move in elliptical orbits, with the Sun at one focus.
When Kepler took into account the date and time of each observation, he found that the planets didn't move at the same speed throughout their orbits, but sped up when they were close to the Sun, and slowed down when they were further away from the Sun. Again, this was known by Copernicus, and didn't surprise Kepler. However, Kepler, with his elliptical orbits, could quantify the variation. Nowadays, we would say that the angular velocity of a planet is inversely proportional to its distance from the Sun, but Kepler was raised in the classical tradition that used geometrical arguments for analysis, and he put it differently. He looked at the wedge of space traced out during a unit of time by each planet at various places in its orbit. When the planet was close to the Sun, it travelled faster, so the wedge was short but fat. On the other hand, when it was far from the Sun, it travelled slower, so the wedge was long but thin. (See Figure 4.)
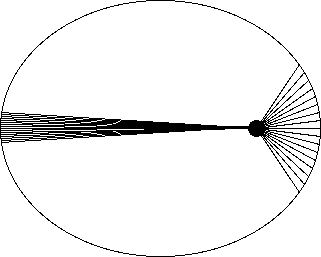
Kepler found that these wedges had different shapes, but they all had the same area. This is Kepler's second law of planetary motion:
Planets sweep out equal areas in equal times.
And I think you'll agree with me that that is a much more elegant way of putting it.
Kepler wasn't done yet. After ten more years, he had analyzed enough data to arrive at his third and final law of planetary motion. The third law was first published in his 1619 book, Harmonices Mundi ("Harmonies of the World"), but was laid out in complete detail, along with the first two laws, in Epitoma Astronomia Copernicanae ("Summary of Copernican Astronomy"). Here it is:
The square of a planet's period of revolution is proportional to the cube of its average distance from the Sun.
Kepler's third law relates the length of a planet's year (its period of revolution, that is) to how far it is from the Sun. The Earth revolves around the Sun in one year (of course), and its distance from the Sun can be expressed as 1 astronomical unit (AU). Provided we express things in Earth years and AU, we can write Kepler's third law as
(1) T2 = r3
where T and r are the planet's period of revolution and distance from the Sun, respectively. So, for example, Jupiter has a period of just about 12 years. If we square 12, we get 144. What number, when cubed, yields 144? About 5.2, and the average distance of Jupiter from the Sun is indeed 5.2 AU.
Kepler published his third law near the end of his life. The rest of his time on earth was spent mostly in non-scientific affairs, such as defending his mother against a charge of witchcraft. He never looked any deeper into planetary motions. He did publish a set of tables of planetary positions based on Tycho's observations, called the Rudolphine Tables, but in comparison with his three laws, the Tables are simple bookkeeping.
Kepler didn't give a causative force that drove the planets in ellipses; he only described their motions. However, that was plenty enough for Isaac Newton (1642–1727) to derive his inverse square law of universal gravitation. Newton once wrote, "If I have seen further than others, it is only because I have stood on the shoulders of giants," and I think, above all, he was thinking of Kepler when he wrote those words. Copernicus may have published the heliocentric model, but it was Kepler who compelled the scientific world to accept it as fact.
And the scientific world has tried to pass that fact down to the rest of us, in abridged form, with such indifferent success that a quarter of American adults seem to have made it up till now without apprehending it.
[1] The 2000 Science and Engineering Indicators, published by the National Science Foundation, if you're curious.Copyright (c) 2001 Brian Tung