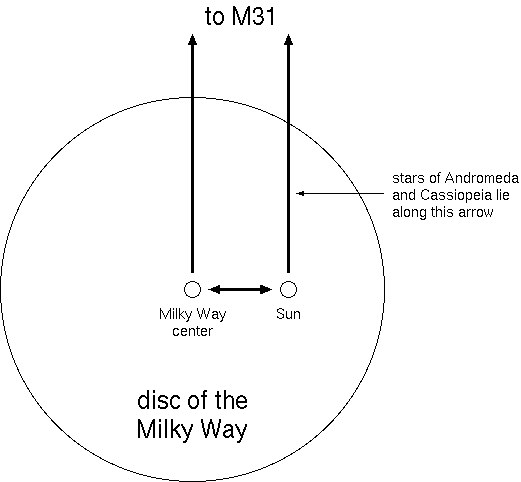
Figure 1. Relative directions of the Milky Way and M31.
Therefore, all things considered, it will be better for me to believe that I am not insane, and go with this gentleman to collect my Prize. If I am wrong, I shall wake up in an institution. There I will apologize to the doctors, state that I recognize the nature of my delusion, and perhaps win my freedom.
—Tom Carmody, in Robert Sheckley's Dimension of Miracles
IN ROBERT Sheckley's Dimension of Miracles (1968), Tom Carmody finds out that he is the winner of a galactic lottery, run by a civilization that until that moment was unknown to humans. He is transported to the center of the Milky Way to accept his "prize," which turns out to be nothing so much as a talking Dear Abby device, whose advice is occasionally bizarre or useless (or both).
Oh, and he also finds out that the trip to the galactic center, to collect his winnings, was a one-way trip. He's on his own for the way back—well, he and his talking advisor.
To quickly summarize the situation, Carmody is oodles of light-years from the Earth, he's been abandoned by the strange people who brought him here, and he has a gadget that, when confronted by a carnivorous dinosaur, advises him to turn himself into a plant.
And somehow, he has to find his way home.
What if this were your problem? To make it somewhat tractable, suppose you're at the center of the Milky Way, and you have a spaceship capable of travelling at, say, 100,000 c—that is, 100,000 times the speed of light, which itself is about 300,000 km/s. The Sun, and the Earth around it, are just about 25,000 light-years from the galactic center. That means that a ship travelling at the speed of light would take 25,000 years to get home, so one travelling 100,000 times faster would take only about 3 months. (We'll ignore the relativistic effects for the time being.)
But you could only get home that fast if you knew precisely where to go. The Milky Way contains some 400 billion stars (give or take a hundred billion or so). The nearest star to our own is Proxima Centauri, a little more than 4 light-years away. If you went through each star in the galaxy, in exhaustive fashion, and each step was 4 light-years long, you would have to travel 1.6 trillion light-years. Even at 100,000 times the speed of light, that would take 16 million years, and let's face it, neither you nor Carmody has that long to dawdle around. Worse yet, over those 16 million years, the stars are bound to move around a bit, and it'll be hard to keep track of where you've been, and where you haven't.
Perhaps, however, the local stars are only spaced 4 light-years apart because the Sun is in, relatively speaking, the boondocks of the galaxy. Stars near the center of the galaxy, where things are busier, are bunched together much closer—perhaps about 1 light-year apart on average. But even if every step was 1 light-year in length, that would still only decrease the total travel time to 4 million years. That's not short enough.
Very obviously, then, if we're going to get home from the center of the galaxy within a single ordinary lifetime, we'll have to make use of some knowledge of the galaxy itself—and only information that we have access to at the current time. No fair assuming that we'll someday have a complete map of the galaxy, down to the last star, and using that instead. The first thing to try, possibly, is that we know we're not at the center of the galaxy, so there's no point in trying all the stars there. And since the galactic center is so tightly packed, that allows us to eliminate quite a few stars.
In fact, knowing that we're approximately 25,000 light-years away from the center means that we don't have to examine any stars out to a distance of almost 25,000 light-years—but not quite. After all, we don't know that figure too precisely. It might be 23,000 light-years, or 27,000; the error bar is, let's say, about 2,000 light-years in either direction. We wouldn't want to skip the Earth just because we happen to be a little off on its exact distance from the galactic center.
If the Milky Way galaxy were a spherically symmetric ball of stars, and we had to systematically check each star in a shell 25,000 light-years in radius and 2,000 light-years thick, we would have to cover a volume of about 20 trillion cubic light-years. At that distance—including our local neighborhood of stars—the density of stars is about 1 star every 50 cubic light-years. That would mean we'd have to cover 400 billion stars, at 4 light-years a pop. As we noted above, that would take 16 million years.
Fortunately, the Milky Way is not a ball of stars, but is rather a beautiful spiral, a little like a pinwheel. In other words, it's flattened out—and rather dramatically so. Estimates vary, but a typical figure is that the disc of the Milky Way is about 50 times wider than it is thick. It's considerably thicker than that at the center, where there's a bulge, but we've already eliminated those stars. Since the Milky Way is about 100,000 light-years across, from edge to edge, the thickness is about 2,000 light-years.
That means that we only have to consider a ring of stars, located at a distance of about 25,000 light-years from the center, 4,000 light-years wide and 2,000 light-years thick. That gives us a volume of "only" about a trillion cubic light-years. Again, at a local density of 1 star every 50 cubic light-years, that means 20 billion stars. At 4 light-years a step, that's about 80 billion light-years, which—at our top speed of 100,000 c—takes us 800,000 years. A lot better than 16 million years, or even 4 million years, but quite obviously not good enough.
The problem is that we don't know which direction to go from the center of the galaxy. If we knew, even approximately, which way to go, that would eliminate a huge part of the ring of stars we have to examine, and shorten the search time commensurately.
A century ago, there would be little we could do. As far as anybody knew, the Milky Way was it, the entire universe. And we didn't even know its structure that well, because even though we get to examine it close up—being a part of it ourselves—that very closeness makes it difficult to get a feel for its large-scale structure. What's more, much of our view of distant parts of the galaxy is blocked out by clouds of dark gas. This gas is actually pretty thin, thinner than a good laboratory vacuum, but because the clouds are so large, and we look through such a great thickness of them, they are very effective at obscuring anything behind them.
If you don't know the structure of the Milky Way, it makes it hard to figure out how to get back home from the center—even assuming you know there to be a well-defined center.
To be sure, there were suspicious looking clouds, called nebula (from the Latin word for "cloud," naturally enough), some of which had been discovered in the middle of the 19th century to display some spiral structure. One of the largest lay in the constellation of Andromeda, and was consequently called the Andromeda Nebula. At the time, these spiral nebulae were thought by most astronomers to be other solar systems in the making; our own Sun was believed to have condensed out of just such a spiraling cloud of gas and dust.
Some believed, however, that they might be other galaxies—"island universes," they were often called—each containing about as many stars as the Milky Way itself contained—and that the only reason they looked nebular (that is, cloudlike) was that they were so far away that no individual stars in them could be made out. At the end of the 19th century, there was no way to tell for sure which idea, if either, was right. No telescope could resolve the nebulae into component stars, and in smaller telescopes they often resembled comets. The comet hunter Charles Messier (1730–1817) put the Andromeda Nebula in his catalogue of comet-like objects (to be avoided when hunting for comets) as M31. The inability to resolve it and other nebulae seemed to imply that they really were clouds of gas and dust within the Milky Way.
As the 20th century dawned, however, a breed of larger and better telescopes was being put into use. The 100-inch telescope at Mount Wilson Observatory, under the command of the American astronomer Edwin Hubble (1889–1953), was the first to be able to resolve the Andromeda Nebula. The overall dimness of those stars demonstrated that M31 had to be very far away indeed—probably hundreds of thousands of light-years, although it was impossible to tell more precisely just from that. At that great distance, it had to be very large and external to the Milky Way. Naturally, there went any idea of it being a solar system condensing out of gas and dust, and from then on, the Andromeda Nebula was increasingly often referred to as the Andromeda Galaxy.
But just how far was M31? In 1912, Henrietta Leavitt (1868–1921), then working at Harvard University under Edward Pickering, was studying a class of variable stars called Cepheids, named after their prototype, delta Cephei, in the constellation of Cepheus the King. She discovered, after analyzing the brightness curves of Cepheids in the Large Magellanic Cloud, a satellite galaxy of the Milky Way in the southern hemisphere, that there was a direct correlation between the period of a Cepheid—that is, the time between its brightness "peaks"—and its average intrinsic brightness.
This made Cepheids useful as standard yardsticks. If all stars were the same brightness, then it would be easy to tell how far they all were; the dimmer ones must be further away, in direct accordance with the inverse square law—but they aren't. It's easy to determine a star's apparent brightness, and if you can find its real, or intrinsic, brightness, you can determine its distance, or vice versa. By timing a Cepheid's peaks, you could determine its intrinsic brightness, and therefore its distance.
Then, in 1923, Hubble followed up his observations of the Andromeda Galaxy by discovering a Cepheid variable in it. After tracking its brightness for some time, he determined that the Cepheid, and M31, were some 700,000 light-years away. That was considerably larger than the size of the Milky Way, and confirmed that M31 was a galaxy, separate from the Milky Way. Later, it was discovered that Cepheids come in different varieties, each with its own distinct relationship between period and luminosity. The Cepheid in M31 was intrinsically brighter than previously thought, and in order to appear as dim as it did, it had to be even further away.
The distance to M31, even now, isn't precisely known, but based on the best available figures, it's about 2.5 million light-years away. Since our estimated distance from the center of the Milky Way galaxy is only about 25,000 light-years, or just about 1 percent as great a distance, M31 is pretty much in the same direction in the sky, no matter where we are in the Milky Way. It therefore serves as a convenient and usable beacon for plotting the first main leg of our trip.
From the center of the Milky Way, M31 is probably not visible—it's lost in the glare of the dense galactic nucleus. We have to go "up," out of the plane of the Milky Way, in order to find it. M31, as it happens, is a bit south of the galactic plane, by about 20 degrees. From the center, we won't necessarily know which way is south, so we'll have to guess. If we guess correctly, then after travelling about 1,000 light-years or so, we'll have cleared the nucleus by enough to see M31.
If, after travelling that 1,000 light-years, we don't see M31, we have to conclude we went up on the north or "wrong" side, and sink back down to the south. By the time we get to the right point, we'll have travelled 3,000 light-years total distance. Since there's a 50-50 chance of going either way, the average distance it takes us, just to find our first beacon, is 2,000 light-years.
Step 1 Distance: 2,000 light-years
Step 1 Time: About a week
What do we do once we see M31? Here, we take advantage of M31's great distance. From the Earth, if we head out of the galactic disc toward the south galactic pole, M31 is in the direction of Cassiopeia and Andromeda, and the center of the Milky Way is out to our left—"at 9 o'clock," so to speak.

But if M31 is so far away, then it will be in the same direction as seen from just above the Milky Way nucleus, too. It will no longer be in the direction of Cassiopeia and Andromeda—those constellations only exist when we observe from the Earth—but they will be in that same direction relative to the Milky Way. If we continue to call the direction of M31 12 o'clock, then from the center of the Milky Way, we should travel toward 3 o'clock to get toward home. (See Figure 1.) It isn't exactly at 3 o'clock, but such a precision is sufficient to get reasonably close. And since home is about 25,000 light-years from the center, that's how far we'll travel in our second step.
Step 2 Distance: 25,000 light-years
Step 2 Time: About 3 months
Assuming that our current-day understanding of the galaxy is correct, we should now be within about 2,000 light-years of home. But that is still far too great a distance to pick out the Sun. The Sun has an absolute magnitude of about 4.8, which means that as seen from a distance of 10 parsecs, or 32.6 light-years, the Sun would appear as a star of magnitude 4.8. Stars of that magnitude are fairly dim and cannot even be seen from many city skies.
But that's as seen from 32.6 light-years away. Two thousand light-years is about 61.3 times further away, and leaves the Sun looking 61.3 squared, or 3,760, times dimmer. A dimming of 3,760 times is equivalent to an increase in magnitude of about 9.0, so from that great distance, the Sun looks like a star of magnitude 4.8 plus 9.0, or 13.8.
Looking for one star like that, out of a multitude, is truly like finding a needle in a haystack. For one thing, if the skies are anything like our own, there are something like a few dozen million stars of about the 14th magnitude. For another, the Sun is unlabelled. There's no tag on the Sun that indicates that the Sun is our particular star. It's an ordinary yellow-white star on the main sequence. Even if we restricted ourselves to those 30 million or so stars that are of about the right brightness and temperature, at least a few thousand could pass for the Sun. We can't spend the time it would take to try each and every one. It's not yet time to resort to trial and error; there's far too much error.
However, if stars themselves are unremarkable, there are other things in the galaxy that aren't. Some objects can't be mistaken for anything other than what they are, and remain so for quite a distance—for much greater a distance, certainly, than any star like the Sun. Many of the nebulae, for example, are quite distinctive. A great many of the nebulae turned out to be external galaxies, which don't help us here, but then, many of them didn't, but really were clouds of gas and dust within our own galaxy. If we could recognize one of them, it might serve as a second stop on our way home.
One of the most noticeable nebulae is the eta Carinae Nebula, in the constellation of Carina the Keel. Carina is one of three constellations created when Argo the Ship (of Jason and the Argonauts) was broken up, and by far the most astronomically interesting of the three. One of the stars in Carina, known as eta Carinae, was known in the early 19th century as an active but otherwise unremarkable variable star. It was ordinarily of the sixth magnitude (that is, barely visible to the unaided eye), but had been known to flare up occasionally to as bright as the third magnitude.
Then, in 1841, it brightened suddenly and dramatically. For a few months, it reached magnitude –1, brighter even than Canopus, which is usually the brightest star in Carina and the second brightest star in the entire night sky, after Sirius. In photographs taken by the Hubble Space Telescope, it appears that in 1849, eta Carinae underwent an explosion that nearly tore it apart. A lesser star would surely have perished; something like 10 or 20 solar masses were lost in an instant, astronomically speaking. In its wake, the nebula around eta Carinae was greatly embellished, and it is easily seen from decent skies on Earth (provided you are well-situated, in the southern hemisphere), even though it is around 10,000 light-years away. From 2,000 light-years, it would be large and obvious.
Unfortunately, being 10,000 light-years from the Earth, it is nearly useless, since we're already within about 2,000 light-years. What we need is something much closer to home—ideally, closer than 1,000 light-years, but we'll accept something a little further away, in exchange for a better fix on our location.
As it so happens, there is a bright nebula that's much closer to the Earth than the eta Carinae Nebula. That is M42, otherwise known as the Great Orion Nebula. This patch of gas and dust, easily identifiable from dark skies as the middle star in Orion's sword, hanging down from the bright belt, is a giant star factory.
The distance to M42 isn't easy to determine. The distance to the stars can be determined using parallax, but that doesn't work as well for diffuse objects like the Orion Nebula. There is, however, another method that takes advantage of M42's known role as stellar birthplace.
The stars in the sky move with respect to one another. They move very slowly, so that it took a long time to discover this movement, called proper motion (and we'll go into how long in just a moment), but they do move. Three of the stars around Orion are called "runaway stars" or "flying stars," for their unusually high proper motions. These motions, if traced back about two million years, point right back to the Orion Nebula. Based on these and other observations, we can determine that the distance to M42 is just about 1,600 light-years. A bit further than we wanted, but certainly an improvement over the eta Carinae Nebula.
Depending on where we end up after Step 2, we'll have to travel an average of about 2,000 light-years to get to M42:
Step 3 Distance: 2,000 light-years
Step 3 Time: About a week
The Orion Nebula, naturally enough, lies in the constellation of Orion the Hunter. The galactic center, where we started, is in Sagittarius the Archer. These two constellations are on opposite sides of our night sky; in other words, the Earth and the rest of the solar system lie right between the Orion Nebula and the galactic center. As a result, by going to Orion, we've overshot our mark. Now we have to trace our way back home, in the direction of the center again, but this time taking a step of only 1,600 light-years—the distance to M42.
You might well wonder why we didn't just go 1,600 light-years less in Step 2, so that we could avoid this next leg. The problem is that we didn't know exactly where we were with respect to home—we might have missed to the right, to the left, up, down, whatever. Only by heading first to M42 can we figure out which way we're off.
Step 4 Distance: 1,600 light-years
Step 4 Time: About a week
We're almost home now—the distance to M42 is known within an error bar of about 100 light-years. From this vantage point, we should be able to recognize quite a few of the familiar constellations of the Earth. Some constellations, on the other hand, will be noticeably altered. The constellation of Canis Major the Great Dog, for example, contains Sirius, the brightest star in the night sky, at magnitude –1.4.
Now, Sirius appears that bright primarily because it's relatively close in interstellar terms: the current estimate is about 8.6 light-years. Its absolute magnitude—again, the brightness it would have at the standard distance of 32.6 light-years—is therefore about 0.0. It's therefore considerably brighter than the Sun, to be sure, but nothing compared with the other bright stars in Canis Major, which are first and second magnitude stars at a distance of 400 light-years and up. Aludra (eta Canis Majoris), at magnitude 2.8, is about 3,000 light-years away. If Sirius were that far away, it would only be a small dot of light at tenth magnitude.
Since these stars are all so far away, most of the shape of the Great Dog will still be recognizable, aside from missing its brightest star. That does not mean that the constellation's appearance will be totally unchanged, and therein lies the key to the last phase of our voyage home.
It's an interesting game to take a photograph of your house, or some other place you're familiar with, and try to figure out the exact vantage point it was taken from. You make an initial guess, say, and stand where you think it might have been taken from. But the picture doesn't exactly match your actual view. Maybe two trees appear too close together; in that case, you'll have to move to one side or the other, so that their separation matches that in the photo. Or maybe a couple of fenceposts have noticeably different heights in the photo, but to you, they appear to be nearly level with one another. Then you have to vary your altitude, again, until the fencepost heights match what you see in the photo.
If you're at the center of the galaxy, there's no way you can play that game with the constellations. The vantage point is too far away. The constellations depend on the lack of depth perception—they contain stars of all different distances from the Earth—and even if you could recognize them in principle, there would be too many stars in the way to pick them out. Similarly, if you had a photograph of your house taken from up in the airplane, it might be difficult to pick out which house was yours, let alone the exact angle and distance of the point where the picture was taken.
But from 100 light-years, things are different. The constellations are close enough to their usual forms to recognize, but not so close that they appear identical. There are enough cues to fine-tune your location. Finally, when you get to within a few light-years of the Earth, the constellation forms might no longer provide a usable basis for navigation, but now Sirius, at a distance of only 8.6 light-years, will do the trick admirably. At that distance, if you're off by a single light-year, Sirius's position in the sky will be in error by as much as 7 degrees, quite easy to notice and adjust for.
Now, it's true that if your position could be off in such a way that Sirius is still in the right position in the sky, but we can address that simply by having a second nearby star to sight. If you know that your house is directly due south of city hall, that alone wouldn't be enough to pinpoint your house's location. Even if you could see city hall to the north, you might be too far or too close to it. But if you also knew that your house was due east of the theater, that would be enough. What we need is a nearby star, one that's unmistakable so that we would recognize it and know where it ought to be, even when it's out of place. What star would be that bright and close to us?
One of the clues that Sirius is so close is that it has a relatively large proper motion. Well, relative is relative; as I mentioned earlier, the stars are mostly so far away that they don't appear to change their relative positioning when you observe them for a year, or for 10 years, or even for 100 years. The proper motion of even the fastest-moving star is only about the width of the full Moon in one century.
Fortunately, humans have been cataloguing the positions of the stars for millennia. The Greeks did it no later than the third century B.C., with Timocharis, and then more famously in the second century B.C., with Hipparchus (c. 190–120 B.C.). Hipparchus had, according to Pliny the Elder, observed a new star—a nova, that is—and in order to accurately record further observations, decided to commit to papyrus all the stars visible to the unaided eye, with their locations and their brightnesses, using the magnitude system that he invented.
Much later, in 1717, the English astronomer Edmond Halley (1656–1742) compared the then-current locations of the stars with those recorded by Hipparchus, and found that the positions of three of them differed by up to half a degree. Such a small discrepancy might easily have been chalked up to the lack of proper instrumentation in ancient Greece, but Halley thought that unlikely, given Hipparchus's other achievements. By taking the old coordinates at face value, he interpreted the discrepancy as an actual change in location, taking place very slowly over nearly 2,000 years. Future observations have vindicated Halley's judgment in this matter.
Because there's no reason to think that these stars were intrinsically different from other stars, astronomers expected that the relatively large proper motion of these stars was due to their closeness, rather than their own native speed through the heavens. What strengthened their case was that the three stars were also quite bright, something else you expect when a star is nearby. One of the stars was Sirius, and the other two were Aldebaran, in Taurus the Bull, and Arcturus, in Bootes the Herdsman.
By using these three stars to calibrate our final positioning, then, we should be able to position ourselves to within a light-year of the Sun and Earth. From that distance, the Sun should be a brilliant star of magnitude –2.7—easily outshining anything else in the sky. That should allow us to head directly home. It's hard to say exactly how far this last step should be, but it's probably no further than the 100 light-years we talked about before:
Step 5 Distance: 100 light-years
Step 5 Time: About 8 hours
All told, adding up all five steps, we cover only a little over 30,000 light-years in just under four months, easily in time for dinner. Not bad!
The imaginary trip we just completed is only convoluted because of our incomplete knowledge of the Milky Way. Galaxies are fluid objects, all of the stars flowing amongst its neighbors, but only on time scales of millions or billions of years. In the short period of time that's needed to get from the galactic center to the Sun in a ship that travels at 100,000 c, we can treat the galaxy as essentially static. For these purposes, it makes sense to think of a "map" of the galaxy.
Such a map may be coming, and relatively soon. The Hipparcos satellite has uncovered the distances to many of the nearby stars to about a several hundred light-years distance. Its proposed successor, the GAIA project, may be able to extend this horizon all the way out to the opposite edge of the Milky Way galaxy. If we had a complete map of the galaxy, we could make it home in a straightforward, one-step trip of about 25,000 light-years.
But oh, what wonders we would miss!
Copyright (c) 2001 Brian Tung