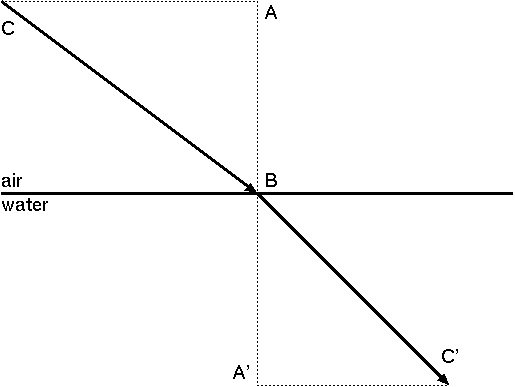
Figure 1. Light entering water from the air.
Light breaks where no sun shines; / Where no sea runs, the waters of the heart / Push in their tides…
—Dylan Thomas
MANY OF the essays I write for this series come out of a question that someone asks about this or that facet of astronomy. Sometimes, I am able to answer the question voluminously off the top of my head, and the questioner invariably goes off with the idea that I am some sort of walking astronomy encyclopedia. For obvious reasons, I love that. (Whether the questioners love it or not is a completely different issue.)
Other times, I find that I have a partial answer, but in order to understand the point completely, I have to consult my references and ask others who know more than I do. As a result of this, I end up knowing considerably more about the topic than I started out, and I can then explain it confidently in one of these essays. As it so happens, I love that too. But I certainly couldn't do it if I didn't have those references and experts to consult [1].
In the case of this particular essay, an innocent question about diffraction on the Usenet group sci.astro.amateur sprouted an endless thread (well, it seemed endless, anyway), and I thought I would try to write something in an attempt to clear some of it up. Not for the active participants, who in any event are too entrenched to give up their (our?) positions, but for the rest who might be wondering what all the fuss is about.
In order to better understand it, however, I had to figure out for myself where the fuss started in the first place. As usual, it started out with something that seemed totally unrelated at first.
From antiquity, it was well-known that water does something funny with the way things look. If you drop a stick in a glass of water, it appears to "break" right where it enters the water. Depending on how you look at it, the stick appears to be bent or snapped entirely in two. The first to investigate this effect systematically was the Greek scientist Claudius Ptolemy (c. 100–170), who measured the various angles by which a stick seemed to be bent as he dropped it in the water this way and that. He attributed this correctly to light bending as it moves from water to air (or vice versa), and today, in consequence, we call this property of light refraction, from a Latin word meaning "to break back." Well, a light ray entering water does appear to bend backward slightly. (See Figure 1.)

Based on his measurements, Ptolemy derived a rule about this bending: Angles ABC and A'BC' are related by a constant; that is,
where n is a constant associated with water. Ptolemy was able to measure this constant, which we call today the index of refraction of water. Its value is about 4/3. Actually, Ptolemy's measurements would have indicated a higher index of refraction as the angles got larger, but the Greeks—never eager to let experimental data get in the way of an elegant mathematical relationship—doubtless let that slide [2].
Such was Ptolemy's influence and sway, in matters physical as well as astronomical, that for 15 centuries, this law of refraction was treated as solid fact. Finally, in 1621, Willebrord Snell (1580–1626), a Dutch mathematician, discovered that angles ABC and A'BC' are not directly proportional to each other. Instead, it is their sines that are proportional:
For many angles, there isn't much difference between the two laws, so perhaps we can be a bit forgiving of the Greeks for thinking they had it right.
Snell neglected to publish his result, and in 1637, the French philosopher and mathematician, Rene Descartes (1596–1650), first put it on a sound mathematical foundation. With Snell already dead for a decade, Descartes saw no need to mention him, and the law was for a brief time attributed to Descartes, until the Dutch physicist and astronomer Christian Huygens (1629–1695) mentioned Snell's priority in a memo written in 1692. Since then, the law of sines has been known as Snell's law. (See what a fat load of good Descartes did himself by not mentioning Snell?)
In 1657, the French lawyer Pierre de Fermat (1601–1665) showed that Snell's law could be deduced as a specific consequence of a more general law, which has come to be known as Fermat's Principle or the Principle of Least Time: Light travels in the path that takes it the least amount of time. Fermat reasoned it out from Snell's law as follows. Light does not travel directly from C to C'. Why not? Because light travels slower in water than in air, and it could save time if it traveled more in the air than in the water. The slower light travels in water, the more it would travel in air, and the greater the bending. In fact, Fermat showed that his principle predicted exactly the same path for light as did Snell's law, provided that the speed of light in water was precisely n times slower than its speed in air. In other words, Fermat deduced that light travels only about 3/4 as fast in water as it does in air.
In actuality, Fermat had no idea how fast light travels in air or in water. That wouldn't be known for another quarter century. (See "Double Vision" for a brief story of how the speed of light was measured.) It is a testament to Fermat's outstanding intuition that he was able to work out his principle with so little data to work from.
The Principle of Least Time has a strange, spectral quality to it. It seems to give light a goal, an objective: that of reaching its destination in the shortest amount of time. How does it know which way to go? And yet this principle is amazingly useful, allowing one to derive a number of optical laws. It can, for example, be used to prove the law of reflection.
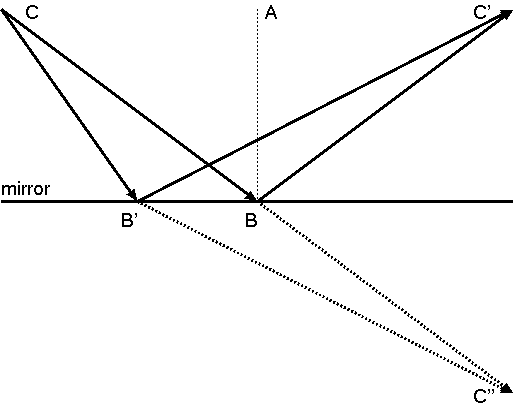
The law of reflection, as applied to the mirror in Figure 2, states that light going from C to the mirror and then reflecting up to C' strikes the mirror at a point B such that the angle ABC is equal to the angle ABC'. Suppose, for the sake of Fermat's Principle, that light does compare all the different points on the mirror for the bouncing point B. How does it know not to bounce off the mirror at B', so that its total path is CB'C'?
Fermat's Principle tells us that it chooses B because that yields the total shortest distance. This becomes clearer when we notice that the path CBC' is exactly as long as the path CBC'', where C'' is the "twin" of C', but on the other side of the mirror. Then it's evident that light must choose the point B that is directly between C and C'', and the law of reflection quickly follows.
It doesn't just work on flat mirrors, either. It also works on curved mirrors. Suppose that instead of a flat mirror, we have a paraboloidal mirror—that is, a mirror that you get by revolving a parabola around its axis. (See Figure 3.)
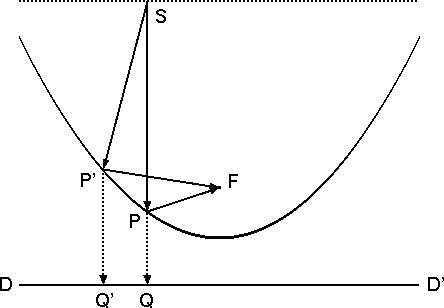
A parabola is a figure that most students learn in desultory algebra classes as the curve generated by the formula, y = x2. But that is only one definition of the parabola. Another definition of it is as the set of points P that are the same distance from a point—the focus, F—and a line—the so-called directrix, DD'.
Suppose a photon at S (reaching us from a distant star) is to bounce off this paraboloidal mirror and make its way to F. (It had better, if we are to see the star in a telescope made with this mirror.) Where should it strike the mirror, in accordance with the Principle of Least Time? If it strikes the mirror at P', then the total distance traveled by the light is SP'F. But by the definition of the parabola, we know that this is the same as the distance SP'Q', where Q' is the point on the directrix directly "under" P.
In a similar way, any prospective reflection point on the mirror can be associated with some path from S to the directrix DD'. But the shortest distance from S to the directrix must be along a straight line straight down to Q. To minimize the total distance and time taken by light to get from S to the focus, light would travel from S to P to F, and Fermat's Principle tells us that that is the path it must take. In fact, note that any point along the dashed line takes the same minimum distance to get to the focus—simply because it's the same as the shortest distance between the dashed line and the directrix.
For that reason, the English physicist Isaac Newton (1642–1727) chose the paraboloid as the shape of his telescope mirror; he knew, for sound mathematical reasons, that all the light from a distant star (or planet or nebula) would travel straight down toward the telescope mirror, and if he used a paraboloid, that light would all bounce up to the focus point as predicted by Fermat's Principle. This point could then be magnified by the eyepiece and viewed by the astronomer as an amplified image of the star (or planet or nebula).
However, that was not what happened. The light steadfastly refused to focus down to a point, but only to a disc of certain size, and the more the view was magnified, the more obvious the disc. At first, this was attributed to the inferior optical quality of the mirrors, but as mirrors became better and better, it became clear that optical quality wasn't the limiting factor. Eventually, it was understood that it was the wave nature of light that was the culprit and that the particular aspect of this wave nature that caused the light to focus down only to a disc was diffraction. Here was an effect wholly unpredicted by Fermat's Principle. Telescopes, it turned out, were diffraction-limited.
But wait! I'm getting ahead of myself. Let's take a different tack…
One of the games I invented for myself as a kid involved an old metal frying pan with a hook, which one could use to hang the pan up—for example, on the long crossbar of a swing set. I would then take a tennis ball and huck it at the pan, which would send it swinging like a bell. If it swung hard enough, the hook would release and the pan would go falling onto the ground. The pan was too heavy for me to get it to fall with one throw of the ball, but several carefully timed throws would do it. You may find it hard to believe, but not only I but some of my friends would go in for this kind of entertainment on lazy summer afternoons. (I find it a bit hard to believe, myself. It probably says something about our childhood.)
Something very quickly made itself apparent: Timing matters. If the pan was still, then you wanted to throw the ball at it as hard as you could. The harder you threw it, the harder the pan would swing. Not hard enough to fall off, perhaps, but enough to give you a good start. On the second throw, however, it mattered not only how hard you threw the ball, but also at what point in the swinging pan's trajectory the ball hit it. If you hit the pan while it was moving away from you, then everything worked out well: the ball's momentum would be added to the pan's, and the pan would swing ever higher.
But suppose the ball hit the pan as it was coming back toward you. Where you'd think the harder you threw the ball, the harder the pan would swing, precisely the opposite would occur. If you hit the pan lightly with the ball, the ball would absorb some of the momentum of the pan and the swinging would diminish, just slightly. But if you hit the pan with the ball really hard, the ball would absorb almost all of the momentum of the pan, and it (the pan) would come to a near standstill.
This is in direct contrast to what would happen if we were to hit a toy truck with the tennis ball. (Goodness only knows what game we would have made out of that.) If you hit the truck once with the ball, it starts to roll forward a little. If you hit it again, the precise timing doesn't matter at all; the truck moves a little faster no matter when you hit it.
We kids were dimly aware that the distinction between the two games was that the truck only moved forward, whereas the pan swung back and forth. Another way of saying that is that the pan's motion is an example of wave motion. What was happening, roughly, was this: The second ball, as it strikes the pan, sets up a second wave motion, which (let's say) is just as strong as the wave motion set up by the first ball. How the pan actually moves is a combination of the two wave motions. If the two wave motions move back and forth at exactly the same times, then they work with each other, and the combination of the two makes the pan swing even higher. Such wave motions are said to be "in phase."
On the other hand, if the two wave motions are not quite in sync with each other, so that the two wave motions don't exactly work with each other, then the swinging doesn't go as high as it does when they're in phase, and we say that these motions are "out of phase." In extreme cases, they work directly against each other, and the pan completely stops. The wave motions are "out of phase by one-half cycle," because one motion moves forward just as the other one moves backward, and the combination of the two is a motionless pan.
Incidentally, where you might think that two in-phase balls would make the pan swing twice as far as one ball does, it actually doesn't swing quite as far—about 40 percent further is as far as it can go. However, the circular arc of the pan's swing means that the bottom edge can swing twice as high (relative to its lowest position, at rest). Let's call the height which it swings represents the "amplitude" of the pan, so that a pan at rest, where the bottom edge is at its lowest position, possesses an amplitude of zero. (Yes, I know I'm defining amplitude at odds with the usual practice. I have my reasons.)
Each ball, then, increases the amplitude of the pan by the same amount—provided that it hits the pan in phase. If a ball strikes the pan out of phase, though, it might add less amplitude to the pan, or even reduce the amplitude of the pan. If you wanted to knock the pan off the hook, you had to be careful to time your throws carefully so that each successive ball hit the pan in phase.
Actually, there is another way to get the pan to fly off, just by throwing tennis balls at it, and we enterprising kids quickly discovered it. Instead of having one person throw balls at it in succession, we could all of us throw balls at it at the same time. That way, all the balls would strike the plate at the same instant (that was the plan, at least), and there would be no issue of timing—the balls would automatically hit the plate in phase.
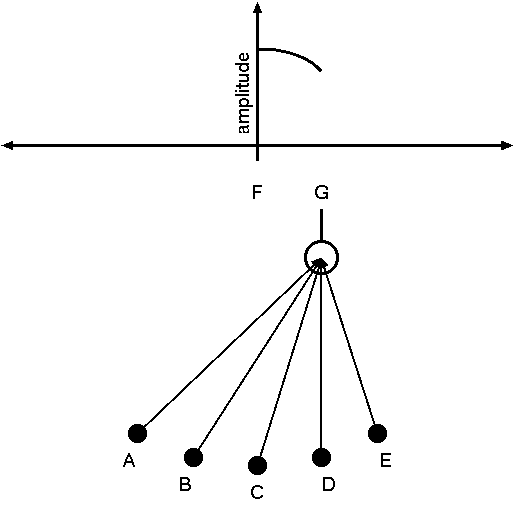
Imagine, if you can stand it, a group of ten-year-old boys arranged in a line, timing their throws to hit the pan at the same time. Now, if they throw at exactly the same time, and at exactly the same speed, the balls won't quite hit the pan at the same time. That's because the boys at the ends of the line are further away from the pan than the boys in the center, and their tennis balls will hit the pan just a split-second late. Instead, if the boys arrange themselves in a circular arc around the pan, then they'll be exactly the same distance away from it, and the tennis balls will all hit the pan at precisely the same time (pang!) and send the pan swinging with all possible speed. This means a maximum amplitude for the pan, when it is at F. (See Figure 4.)
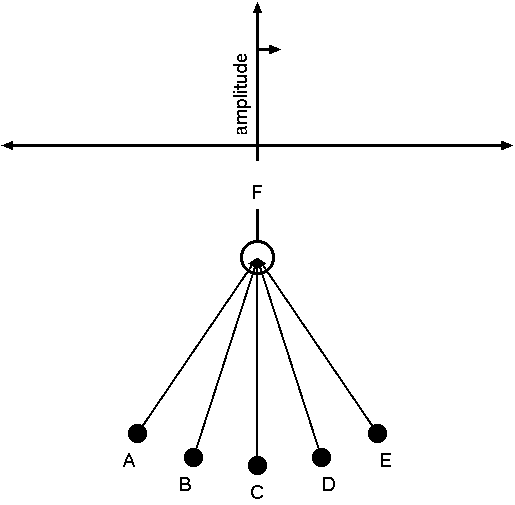
Next, suppose that we leave the boys where they are, but move the pan just a little bit out to the side, to G. Then, the boy at A is just a bit further from the pan than before, and the boy at E is just a bit closer to the pan than before. If the boys throw their tennis balls at exactly the same time, and at exactly the same speed, the balls will no longer hit the pan at the same time. Instead, they'll be just a bit out of phase, and the pan won't swing quite as high as before—the pan's amplitude is just a bit lower. (See Figure 5.)
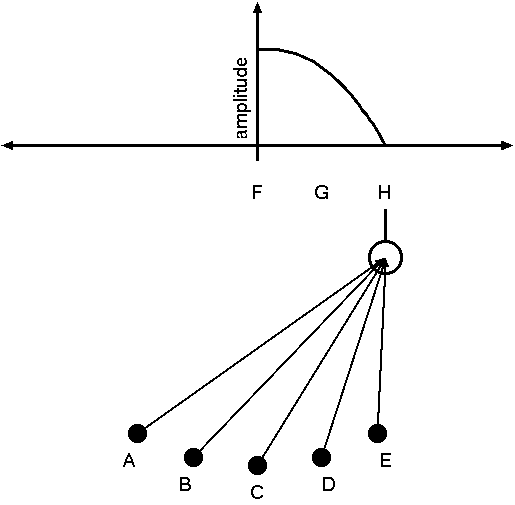
If we move the pan further out still, the balls will hit it even more out of phase, and the amplitude of the swinging pan goes down again. Finally, if we move the pan far enough out, to H, the balls will strike the pan so far out of phase with each other that their effects will precisely cancel out, leaving the pan hanging motionless. The pan's amplitude is then zero. (See Figure 6.)
If we move the pan out just one more time, to I, a curious thing happens: the pan starts swinging again! How does that happen? The balls from A and E are so far out of phase with the balls from the center (at C) that they begin to be in phase with each other, and they make the pan swing. The tennis balls only work partially in phase with each other, however, so that the swinging is not very intense—perhaps only a small fraction as high as before. (See Figure 7.)
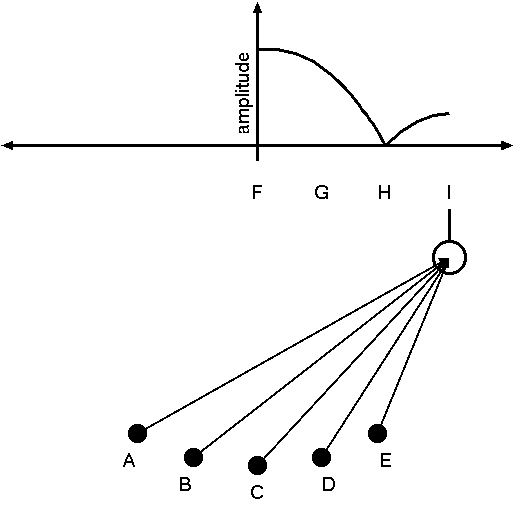
If we continue this exercise further out in both directions, we get an amplitude curve that looks a bit like a bouncing ball, centered at the point where the pan is at the center, plus a few smaller extensions on either side. These wavy extensions quickly dampen out, however, so that for the most part, only the central bounce is really prominent. This curious behavior, believe it or not, is the simple result of having a few boys throw balls at a frying pan at different points.
All well and good, but what does this have to do with diffraction and telescopes?
If you examine Ptolemy's law of refraction, or Snell's law, or Fermat's Principle of Least Time, you'll see that each treats light as if it were a stream of particles. At any moment these particles have a definite location, and they travel from location to location at the speed of light (what else?).
If light is a stream of particles, then it stands to reason that if you hold a square piece of cardboard in front of a screen, and project light at it, you'll get a square shadow. If the light source is a point source, then the square shadow should be perfectly sharp, since the cardboard should block all the light that is headed in its direction, and leave completely unaffected the rest of the light, even the light that just barely misses it. Furthermore, if you cut a small, thin window in the cardboard (like an arrow slit), you should get a perfectly sharp thin sliver of light from the light that passes through it. This seems so obvious that it doesn't even bear testing.
However, as long ago as about 1500, there were signs of problems with this simple view of light. Shadows created under such conditions were not perfectly sharp, as it turned out, nor did they smoothly dim out to darkness. Instead, near the edge of the shadow, there were fluctuations that could not be attributed to the uneven edges of the cardboard (or whatever cast the shadow). This was alluded to, briefly, by Leonardo da Vinci (1452–1519), but the first direct description of this effect was given in a posthumous publication by the Italian mathematician and physicist Francesco Grimaldi (c. 1618–1663).
In his writings, Grimaldi describes how he stuck a rod into a thin beam of light shining into a dark room. To his surprise, the rod cast a shadow that was wider than he expected. Moreover, the edge of the shadow had bright and dark fringes, reminiscent of water lapping on a beach. To Grimaldi, the light just at the edges of the shadow appeared as though it had been broken into pieces, so he called the effect diffraction, after a Latin word meaning "to break apart."
These and other experiments seemed to suggest that light really behaved as though it were a wave. This led to the conception of light developed by Huygens, in which a light source emits a spherical wavefront of light, like ripples spreading out from a point on a pond's surface. Each point on the wavefront is in phase with every other point on that wavefront; if one point is cresting, so are all the other points on that wavefront. According to this conception, furthermore, each point on each wavefront is the center of a new spherical "sub-wavefront" of light [3]. So long as the light is unobstructed (by a piece of cardboard, say), these new "sub-wavefronts" combine and interact, in and out of phase, to generate the "next" wavefront, as seen below in Figure 8:
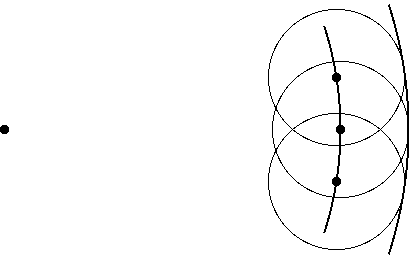
If something does block the light, however, then the "sub-wavefronts" that would have been generated by the light blocked by the cardboard aren't available to interact, and the light that does just barely get by the cardboard, no longer interacting with the blocked light, produces those puzzling diffraction effects seen at the edge of the shadow. In this sense, diffraction effects aren't exactly due to the edge of the cardboard, but they are seen at the edge of the shadow.
In fact, the same goes for mirrors: each point on the surface of a mirror is a new light source, with its own spherical wavefront. This, in a way, solved the old question of how light knew which way to go; it didn't, but instead it tried every way of going. But then, why does it look as though it only goes the fastest way? Why does light bouncing off a flat mirror appear to take only the path CBC' (refer back to Figure 2), rather than bouncing off all the other points on the mirror?
Huygens, and later the French physicist Augustin Fresnel (1788–1827), answered that by saying that although the light goes every which way off the mirror, only the light near the point B goes to the point C' in phase. All the light from the rest of the mirror arrives out of phase and essentially has no effect. In fact, if we chop out everything but the part of the mirror near B, the light arriving at C' from C is essentially unaffected.
However, a flat mirror has no focal point. What happens with a paraboloidal mirror, which does have one? The reason why the light is so intense at the focus, according to the particle theory of light, is that all the particles of light converge there. According to the wave theory of light, however, not all the light goes there, but all the light that does go there, gets there in phase. It all adds up, rather than subtracting from itself.
The reason for this is that even though light from a distant star travels outward toward the Earth in a spherical shell, the star is so far that by the time the wavefront gets to, say, the top of the telescope, it is as flat as a piece of paper (much as any small section of the Earth is flat, if we neglect local variation).
If we point the telescope directly at the star, this wavefront comes in parallel to the directrix of the mirror—in other words, just like the dashed line in Figure 3. But as we saw earlier, that means that each point on the wavefront takes the same time to get to the focus, and if they all start out in phase with each other, they all get to the focus in phase with each other. The amplitude of light at that point will then be at its greatest, just as the amplitude of the frying pan was at its greatest when the pan was at the center point in front of the boys.
Also, just as the frying pan's amplitude went up and down as we moved it from side to side, and the tennis balls arrived more or less in phase with each other, the same thing happens with the light. The light does go to those other points after all, but some parts of the wavefront get there out of phase with other parts, and to varying amounts, so those points appear dimmer than the center point, to varying amounts. If we look a certain distance from the center, in fact, the light arrives at all amounts out of phase and we see no light there at all. That corresponds to a stationary frying pan.
There's one more wrinkle. The way that I defined amplitude for the frying pan, the pan's energy is proportional to the amplitude, but for light, energy is proportional to the square of the amplitude. Our eyes see the energy (more properly, the intensity) of the light, so the pattern of light seen by our eyes looks like the bottom curve in Figure 9:
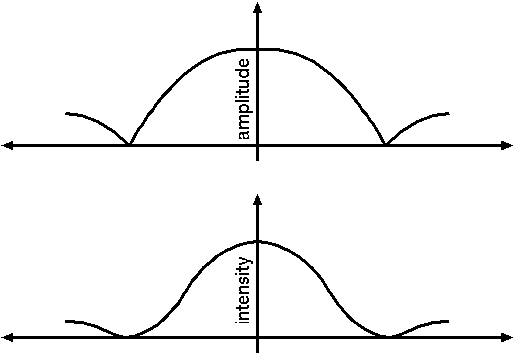
That is the diffraction pattern created by light from a distant star, interacting through the wave nature of light. That is what astronomers, looking through a good telescope at a distant star, saw in place of a point of light, and it was one of the crowning moments for the wave theory of light.
Because of diffraction (and also because of other behaviors of light), the wave theory of light took ascendancy throughout the 18th and 19th centuries, culminating with the four laws of electromagnetics put forth by the Scottish physicist James Clerk Maxwell (1831–1879), which seemed to confirm that light was an electromagnetic wave. It was unclear what medium the light was waving through, and a so-called "luminiferous aether" was proposed to carry electromagnetic waves. If there was such a thing, then there should be some frame of reference where the aether is stationary, and the speed of light shown to be its nominal value. The Michelson-Morley experiment, designed to detect this frame of reference, ended up showing that there was no aether at all—light apparently could traverse empty space after all.
It was not until the 20th century that Einstein showed that the photoelectric effect could be explained by assuming that light was made of particles called photons. This created a seeming inconsistency in the nature of light, which was not completely bridged until the development of quantum electrodynamics, in which photons, although they are particles, also have a kind of phase to them (much like the tennis balls!). But that's a matter for another essay…
[1] This might make it sound as though I place all the responsibility for being correct on the references and the experts. Not at all! I choose my references and experts carefully enough that I am quite confident that they have it right, and if I get it wrong, it is only because I have unfaithfully reproduced their meaning. And then someone writes to correct me, and I even love that (mostly, he says, hedging a little). I can't lose.
[2] Since this was written, I've read that Ptolemy actually measured angles that were a little off, which would actually have fit better with a law of sines, but he fudged his data so that they would fit the law he had already decided on. If he hadn't been so convinced he was right, we would be speaking of Ptolemy's Law of refraction, and not Snell's.
[3] Actually, there's a little more to it than that. A point source of light may radiate light equally in all directions, but the "sub-wavefronts" do not. They are weighted forward in the direction they were going. This prevents nonsensical effects such as light arbitrarily radiating backward out of nowhere.
Copyright (c) 2002 Brian Tung