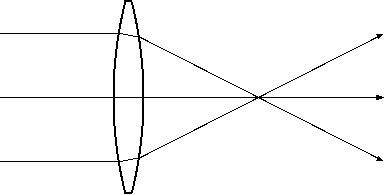
Figure 1. Refraction produces a focusing lens.
Through gloom and shadow look we / On beyond the years: / The soul would have no rainbow / Had the eyes no tears.
—John Vance Cheney, Tears
THAT GREAT Greek poet, Homer, if he existed at all, was responsible for two of the most majestic literary epics of the classical world: the Iliad and the Odyssey. They tell the story of the Trojan War and of Odysseus's long travels, and they are written almost entirely in verse.
Of course, when I say written, I really mean cobbled down. One of the reasons that Homer's existence isn't 100 percent certain is that we don't have independent corroboration that some person named Homer sat down and wrote every last omega of the two works. The stories were handed down in oral tradition for a long time before they were written.
Just the same, those two works were held, even in classical times, in high esteem, and the Greek in which they were written is known as Homeric Greek. A few centuries later, they were translated into Latin, at least in part by the famous Roman poet, Horace.
In so doing, Horace discovered, somewhat to his annoyance, that there were several places in which Homer seemed to have erred, and for that reason, he wrote the famous words, bonus dormitat Homerus, Latin for "Even Homer nods." But he then went on, almost in the same breath, to make an excuse for Homer, since "it is almost inevitable that in such a long poem some slumber should come."
By the way, when Horace spoke of Homer nodding, he wasn't talking about anything so mundane as Homer getting his facts wrong. Since Homer was the source of practically all accepted history of the Trojan War, he was almost by definition right on matters of fact. Instead, Horace meant that Homer seemed to have violated the rules of rhyme and rhythm.
There's a good explanation for that. By the time Horace rolled around, the contemporary Greek had mutated into a new version, called Attic Greek. Although the two versions were mutually intelligible for the most part, there were differences. Syllables were dropped, others were run together (as we do when we write and say "do not" as "don't"), so that what used to run smoothly in Homeric Greek became ever so slightly choppy in Attic Greek. In other words, when Horace wrote that even Homer nods, he was really just detecting the change that Greek had undergone in the intervening centuries—although he had no way of knowing that.
Science has its Homer, too, and his name was Isaac Newton. He lived from 1642 to 1727, and over his long life, he managed to make seminal contributions to a wide range of fields: mathematics, mechanics, thermodynamics, astronomy, and optics, to name a few.
Even Newton nodded, though, and in hard fact rather than prosody. For example, he invented a new kind of telescope, which for about 200 years was the choice of large instrument for serious observers. The reason he created this telescope, however, was that he had made a conclusion about the way light interacted with glass—a conclusion that, as it turns out, was mistaken. But to understand how he came to this conclusion, let's go back a century earlier, to the development of the astronomical telescope.
The telescope seems to have been invented around 1608 by a Dutch optician named Hans Lippershey (1570–1619), although there are some hints that others may have come close before him. The following year, the Italian scientist Galileo Galilei (1564–1642) heard enough about the design of the telescope to put together a few of his own and, for the first time anywhere in the world, pointed it at the sky. He made many astonishing discoveries: craters and mountains on the Moon, sunspots on the face of the Sun, the four big satellites of Jupiter, and the phases of Venus—all within the span of a couple of years. These discoveries went a long way toward striking down the Ptolemaic Earth-centered system and establishing the Copernican Sun-centered system.
Galileo's telescope was by today's standards a very poor one, even though it allowed him to make all those observations. Even putting aside the imperfections in how the telescope was put together, Galileo used a design that has some debilitating flaws. His telescope consisted of two lenses, both of which bend or refract (see my essay entitled "Diffraction") light as it passes through them. Therefore, this general class of telescope is known as a refractor. In Galileo's design, the bigger lens or objective—the one pointed toward the sky—is a convex lens, in which both sides bulge outward, and the smaller lens or eyepiece is a concave lens, in which both sides are bowed inward.
For reasons we won't go into here, this design results in a narrow field of view; Galileo's first telescope only allowed him to see a section of sky as wide as a strand of spaghetti held at arm's length. (In contrast, most of today's small telescopes will allow you to see a section of sky as wide as your thumb held at arm's length.) Moreover, the view at the edge of the field was blurry and distorted, so the usable field of view was even smaller than it would have been otherwise.
Then, in 1611, the German astronomer Johannes Kepler (1571–1630) discovered a way around some of these problems. His design used a convex lens for both the eyepiece and the objective, and it permitted a wider field of view, as well as lower levels of distortion around the edges of that wider field of view. The only cost was that the view was inverted, as compared to the unaided field of view—a problem for terrestrial objects such as distant mountaintops or faraway enemy ships, but hardly an impediment to observing astronomical objects, where the notion of up and down held little intrinsic value. Kepler's innovation greatly influenced the future of optical astronomy—in fact, practically all refractors in use today, for astronomical purposes, have their basis in Kepler's design.
Kepler's improvement didn't solve everything, though. Specifically, the design was still susceptible to a problem called chromatic aberration. Around all bright objects was a purple fringe. You can get a hint of this if you look through a pair of inexpensive binoculars toward the Moon, but it was much worse in Kepler's day—so bad, in fact, that it greatly affected the level of detail that astronomers could see.
Astronomers went to great lengths—literally—to get around chromatic aberration. Somehow it was found that images exhibited lower levels of chromatic aberration when they were made longer. This led to the development of longer and longer telescopes. The trend was gradual; at first, a long telescope meant one that was merely 6 to 10 feet long. Then the bar was raised to 30 or 40 feet. Eventually, the Polish astronomer Johannes Hewelke (1611–1687), better known by his Latinized name, Hevelius, built refractors that were as long as 150 feet. They required elaborate systems of pulleys and levers to maneuver, for in the endeavor to reduce the effects of chromatic aberration, they were built so long that they reduced the field of view to ridiculous extremes, and the pointing system had to be overbuilt to provide the precision needed to keep the target in view as it crossed the heavens.
But why? Why do refracting telescopes show so much chromatic aberration? Why does building them longer reduce these effects to some degree? And what else can be done about this problem? The first and last of these questions were answered by the greatest scientist the world has ever known, Isaac Newton.
Newton is best known for his three laws of motion and his law of universal gravitation (see "The Grand Illusion"), but he also performed seminal investigations into the nature of light. These were summarized in his book, Opticks, written, in English (a rarity for scientific works in those days—most serious work was written in Latin), over the first years of the 18th century.
In particular, Newton performed experiments to show that white light actually consisted of light of various different colors, like the colors in a rainbow. He showed that a glass prism—a piece of glass shaped like a triangular bar—could be used to break white light into its constituent colors: red, orange, yellow, green, blue, violet. He also anticipated that many detractors would charge that it was the glass that produced the colors, rather than dividing up white light—which was obviously colorless, even to an idiot—into its purportedly colored components. So he showed that multiple prisms could be arranged so as to first separate light into different colors, and then combine them back into white light again, thus showing that the glass could not alone be responsible for the colors.
Why does this happen? The reason, as was later found, is that glass refracts light. If light strikes a piece of glass face on, the light continues on in its original direction. If, however, the light hits the glass obliquely, at an angle, then the light is deflected, by an amount that depends on how obliquely the light entered the glass in the first place. In an ordinary piece of plate glass, if the light comes in at an angle, it is bent as it passes through the glass, but once it exits the glass, it unbends by exactly the same amount as it did when it entered the glass—provided the glass is truly flat—and the total effect is small. (Nonetheless, it can be seen. Try looking at a scene through a small section of plate glass as you turn the glass this way and that. You should be able to see the view no matter how you face the glass, but you can see the image shift by a small amount depending on how much you turn the piece of glass.)
However, a lens in a telescope is not flat—by design. Instead, in a convex lens, it is curved one way on one side, and the other way on the other side. The upshot is that light is bent as it enters the glass, but is not unbent as it exits the glass. Instead, it is bent even further in the same direction. This behavior is what allows the lens to focus light from a bundle of parallel rays into a single point. (See Figure 1.)

The amount of bending is determined by something called the index of refraction. This index tells you how much light is slowed down by entering the lens, and the higher it is, the more the light is bent. For example, for typical glass, the index of refraction is 1.5. That means that light entering a piece of glass is slowed down by a factor of 1.5; light travels 1.5 times faster in air than it does in glass. When light goes from a material with a smaller index of refraction, such as air, to one with a higher index, such as glass, it bends one way. When it goes from higher to lower, it bends the other way—provided the boundaries between the two materials are oriented the same way in both cases.
When the boundaries are oriented in opposite directions, as they are in a lens, the effect is to bend light twice in the same direction. This is what enables the lens to focus light.
Unfortunately for telescope makers, the index of refraction is ever so slightly color-dependent. Typically, it is higher for blue light than it is for red light, meaning that blue light is bent more than red light is. As a result, when you pass a bundle of parallel light rays through a lens, the blue rays come to focus faster than the red rays do. (See Figure 2.) So there is no one single focal point of the telescope lens; there is, at best, a focal point for each color of light. This is also why a prism is able to break up white light into its constituent colors, except of course that that is its intended purpose, whereas with a lens, you'd like to keep all the colors together.
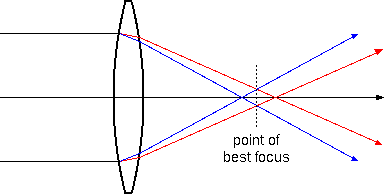
The human eye is not equally sensitive to all frequencies or colors of light. It is more sensitive to green light, all other things remaining equal, than to either red or blue light. Green light is intermediate between red and blue, and is therefore bent more than red light, but less than blue light. Because the eye is more sensitive to green light, the nominal focal point of the lens is chosen to be the point at which green light comes to a focus. It is at that point that you try to focus the telescope—that is, so that the green light from the object comes in sharply.
What happens, at that point, to the red and blue light from an object? The red light comes to focus slower than the green light, so when it reaches the nominal focal point of the telescope, the red light rays have not yet converged to a point. They are still distributed around a small interval around the center, where the green focal point is.
Conversely, the blue light comes to focus faster than the green light. Before light reaches the nominal (green) focal point, the blue light rays have already converged to a point. By the time we get to the focal point, those light rays have already passed focus and are diverging again. They too are distributed around a small interval around the center. The size of the disc in which red and blue light is distributed at the focal point is called the chromatic blur.
Thus, if we were to observe a white star in the telescope, the green light from the star would come to focus at the nominal focal point, and would appear as a point. But the red and blue light rays would only come out as a blur around that central point. Since we see a red and blue light as combining to make purple, this accounts for the purple fringe seen around bright stars.
This property of color separation is called dispersion. What if we could somehow reduce the effect of dispersion, to make the angle by which red light is bent differ less from the angle by which blue light is bent? Unfortunately, the only way to do this with ordinary glass is to reduce the curvature of the glass. If we make the lens flatter, then the red and blue light rays diverge more slowly, it is true, but the focal length of the lens—the distance between the lens and its nominal focal point—becomes longer. There is therefore more distance for the red and blue light rays to separate, even though the rate at which they diverge is lower.
The two effects counteract each other, so that for any given size of the objective, no matter how flat that objective is and how long its focal length, the chromatic blur will be the same size. Typically, the chromatic aberration for this kind of lens is about 1 part in 50; this means that the chromatic blur is 1/100, or half of 1/50, of the diameter of the objective. (It's half of 1/50 because the nominal focal point is halfway between the red focus and the blue focus. If we focused the scope for blue light, the red blur would be 1/50 the diameter of the objective, and vice versa.)
But if the chromatic blur is the same no matter how long the focal length is, then why bother with ridiculously long telescopes, as Hevelius did? The reason is that there is more to it than chromatic aberration. Diffraction (see, again, "Diffraction") also spreads light around, and in a way that doesn't depend as strongly on the frequency or color of light. Its linear size does depend, however, on focal length. The longer the focal length, for any given size of lens, the wider the diffraction disc, or circle within which diffraction distributes light. As you make the focal length longer, the growing diffraction disc overtakes the constant-sized chromatic blur, so that chromatic aberration becomes a diminishing concern.
Of course, there's a limit to how long you'll want to make your telescope. Even if you could build a perfect mount that would track an object exquisitely at any power (which is an impossibility itself), the tiny field of view afforded by a telescope 150 feet long makes it difficult to get the darned thing pointed at the object in the first place.
Perhaps, Newton thought, you could add a second lens. The second lens would be a concave one, which diverges rather than converges light. In such a lens, blue light is still bent more than red light, but now it would be bent out more than red light, instead of being bent in more. Maybe the two effects would cancel themselves out and leave a lens that affects all light equally.
Unfortunately, Newton concluded, there was no such second lens. No matter how you arranged things, if the second lens exactly cancelled out the chromatic aberration, it would also exactly cancel out the focusing property, making it as ineffective as a flat piece of glass in producing an image. For the image to appear in the eyepiece, chromatic aberration had to rear its ugly, multicolored head, it seemed.
The problem is that most glass has the same index of refraction, around 1.5. Adding the second lens is, in most cases, no different from just adding more glass to the first lens. Since there's no way to shape a single lens to get cancel out the chromatic aberration, Newton concluded that there was no way to add more lenses to do that either.
But here Newton erred—he nodded, and in a way that he should have known better. [1] Not all glass has the same refractive properties. Some glasses, called flint glasses, have a higher index of refraction—about 1.6 to 1.7—and their variation by frequency or color also goes up accordingly. Ordinary glasses, with indices of refraction around 1.5, are called crown glasses. (The actual distinction between flint and crown is based on the amount of dispersion, but for most glasses, dispersion varies with index of refraction in a predictable way. I make implicit use of that in what follows.)
This allows us to construct an objective for a refractor that largely cancels out the chromatic aberration. Remember Figure 2, which showed how blue light comes to nearer focus than red light does? The problem is that when light enters the lens, the surface of the glass is oriented one way, and when it exits the lens, the surface is oriented the other way. The result is that both times, the blue light is bent inward more than the red light.
To get rid of that, we want the blue light to somehow get outside the red light within the lens, so that when the two colors exit the lens, they will be on convergent paths. But how do we do that, short of curving the air-glass boundary the same way twice, which as we've seen would eliminate the focusing ability of the lens?
The trick is to make the light act as though it's coming from a material with a higher index of refraction, rather than one with a lower index, such as air. This reverses the color dependency of the refraction, pulling the blue light to the outside of the red light. And the best way to make the light act as though it's coming from such a material is to actually make it come from such a material!
Here's one way to put it together. In front of the single convex lens, let's add a second lens that is flat on the front face, and concave on the back face, such that it mates perfectly with the original lens. (See Figure 3.) This is actually the reverse of the way that most such objectives are assembled today—usually the light enters the curved side and exits the flat side—but this actually doesn't affect the operation of the lens very much.
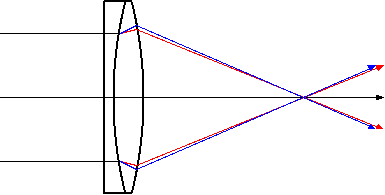
When light from a distant star hits the new front lens, it does so face on. As a result, it isn't bent at all. It continues on to the rear lens just as it did before.
But now, when it strikes the flint-crown boundary, the change in index of refraction goes the opposite way from when it was an air-crown boundary. As a result, the way the colors bend is the reverse of what it was before. The blue light bends outward more than the red light. When the light exits the original crown lens, it does the usual thing and the blue light bends inward more than the red light. By tuning the curvatures of the two lenses, the two effects can be made to counteract each other and the end product is a lens that does, more or less, the same thing with all colors of light, and yet is still able to focus light to produce an image.
This kind of compound lens is called an achromatic lens, or achromat for short, from Greek words meaning "without color." It has an interesting history; the first person to get the idea that this sort of trick might be possible was the English barrister Chester Hall (1703–1771), in 1733. In an effort to keep it secret, he contracted two separate opticians to make the two component lenses. In those days, as in current times, it was common for opticians to farm their work out elsewhere, and unfortunately for Hall, both of them subcontracted the actual lens-grinding work to the same contractor, George Bass (1733–1769). Bass received the two orders at almost the same time, and noticed that they were the same size and fit each other almost perfectly. Once he had ground and polished the lenses, he put them together and discovered what Hall was after. He even built a telescope using the achromatic lens, but didn't develop it any further.
Then, in 1758, Bass encountered the English optician John Dollond (1706–1761). Dollond reintroduced the concept of the achromatic lens in a paper to the Royal Society, England's scientific board, and eventually was granted a patent, one that he himself did not aggresively defend. He did, however, have an optical instrument company named Dollond and Sons, and after control passed to his sons, they did prosecute a few cases of patent infringement.
In time, the art of designing achromats reached its apex with the Bavarian optician Joseph von Fraunhofer (1787–1826), who essentially created the design we know today. His lenses were highly sought after by the wealthy astronomers of his time, and he was able to create objectives as much as 9 inches in diameter with tolerable chromatic aberration.
Tolerable? Yes: Even with Fraunhofer's enhancements, the achromatic doublet, as the two-lens combination came to be known, did not completely eliminate chromatic aberration. At best, it reduced it by a factor of about 40, to one part in 2,000. This made it possible to produce refractors of moderate length that performed well, but as astronomers got used to this higher level of color correction, they began hankering after something even better…
But that's another essay in itself!
[1] We shouldn't complain too much: Because of his albeit erroneous conclusion, Newton designed and constructed the famous Newtonian reflector. This kind of telescope uses no lenses at all, besides the eyepiece, only mirrors. Mirrors reflect light equally for all colors, so there is no dispersive effect in a Newtonian reflector, and no chromatic aberration.
Copyright (c) 2003 Brian Tung