A lot is often made, especially by refractor owners, of the large central obstruction of Schmidt-Cassegrain telescopes in general—and to a lesser degree, Maksutov-Cassegrains as well—and of the C5+ in particular. The C5+ is a 127 mm clear aperture telescope with a 50 mm obstruction, which works out to about 39 percent. That's 39 percent by diameter, which means it's about 15 percent by area. In other words, 15 percent less light works its way into the C5+ than would if there were no obstruction at all.
Now, 15 percent may not sound like a lot; in fact, a scope that has a 4-1/2 inch clear aperture and no obstruction would gather less light than the C5+. But the effect of that central obstruction is not simply to reduce the light gathering power of the C5+. No, there is a more insidious consequence of the secondary, and that is to lower contrast.
Why does this happen? It starts with the Airy pattern. The Airy pattern refers to the image of a point source (which a star is, for all intents and purposes) through perfect optics. Even through the hypothetically perfect telescope, a star doesn't appear as a single point of gleaming light. Instead, because of the wave nature of light, what you get is a central disc—the Airy disc—surrounded by diffraction rings, so that the entire image looks a little as though you were seeing Saturn from above. The Airy disc is always present, although it's hard to see for the first time with powers under perhaps 125x or so (with the C5+).
There's a whole body of literature devoted to the Airy pattern. But here's the scoop with regard to contrast. Through an unobstructed telescope (such as a refractor), 84 percent of the light goes into the Airy disc, and the other 16 percent goes into the rings—and most of that goes into the first ring just outside the disc.
Through an obstructed scope, however, less light goes into the disc, and more goes into the rings. The larger the obstruction, the more the light is transferred from the disc to the rings. Through the C5+, for instance, just 59 percent of the light goes into the disc proper.
What does all this have to do with contrast? Well, it means that through a refractor, the light from any spot is more concentrated, and through an SCT (like the C5+), it's more spread out. Imagine looking at, say, Jupiter, but through one of the scopes, each point of light is spread out—smeared, so to speak. You can imagine quite easily that small features especially will be blurred more in the obstructed scope than in the unobstructed one.
It's more complicated than that, though. All other things being equal, an obstruction degrades the image, but all other things are not always equal. The diameter of the disc and the spread of the diffraction rings gets smaller as the aperture gets larger, so even though an 8-inch SCT has more of its light in its diffraction rings, those diffraction rings may lie almost entirely within the Airy disc of a smaller 4-inch refractor.
What's more, the price and portability of the C5+ usually put it in direct competition with smaller refractors, rather than those with a 5-inch aperture. The increased aperture and the obstruction might just cancel each other out in the contrast department, and the C5+ will still have greater light-gathering power.
A mathematical relation called the point spread function tells you how intense the light is at a certain angular distance from the center of a star. The analysis of the central obstruction's effect involves Bessel functions, which I won't bore you with. Here's a summary, though.
As expected, the light intensity is greatest at an angular distance of zero, at the center of the Airy disc, drops off to 0 at the edge of the disc, brightens again for the first ring, drops off to 0 at the edge of the first ring, brightens again for the second ring, and so forth. I used the formula to calculate the effect of the 39 percent central obstruction, and to compare it against a number of unobstructed scopes of similar or smaller apertures. Below is a graph of the results:
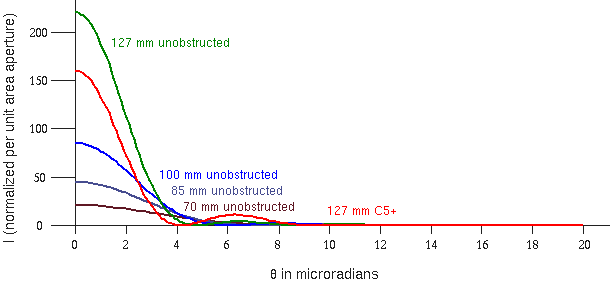
The curves represent the light intensity at a given "radius" from the center of the Airy disc, that radius being really the angular separation from the center of the disc. (Here that angle is measured in microradians, since that allows me to deal with pi, instead of pi mixed with some power of 60. For reference, a second of arc is about 5 microradians.) I should add that these calculations were based on blue-green light with a wavelength of 500 nm.
Curves are shown for the C5+ (red), a 5-inch refractor (green), a 100 mm (about 4-inch) refractor (dark blue), an 85 mm (about 3-1/2 inch) refractor (pink), and a 70 mm (about 2-3/4 inch) refractor (light blue). These sizes do exist: Meade makes a 5-inch apochromat, and TeleVue makes apos and achros in the other three sizes. The Ranger and Pronto, for instance, are 70 mm scopes.
What you notice is that although the C5+ is the only one with a pronounced first diffraction ring, its central peak is brighter than any of the others, except of course for the 5-inch refractor. Not only that, but (and admittedly this is hard to see), the first diffraction ring of the C5+ fits almost entirely within the Airy disc of the 70 mm scopes. This suggests that the contrast in the C5+ is perhaps better than many of the scopes in its price class.
But enough of this theory: what really happens when you take these telescopes in the field?
I haven't had a chance to compare it with too many refractors, but from what I have seen, I think the C5+ would probably beat at least an average 85 mm refractor in the contrast department, and it might hold its own with many of the 100 mm refractors. Obviously, much is going to depend on the quality of the refractors. By most accounts, the C5+ and its siblings are typically good but not great 5-inch SCTs.
According to Terence Dickinson, writing in The Backyard Astronomer's Guide, a traditional test of good optics and good seeing is the ability to see the small craterlets in Plato, a medium-sized crater in the northern part of the moon. These largest craterlets are about three kilometers across, and are made somewhat more difficult by the fact that Plato is closer to the edge of the moon's disc than not. Dickinson writes of them that they "have been detected by 4-inch refractors." Recently, on a night of very good seeing, I was able to pick them out through the C5+. I wouldn't even say that they were difficult or doubtful. This suggests to me that the central obstruction isn't fatal to the resolution and contrast of images through the C5+.
Here are a few other low-contrast features that I've been able to discern through the C5+:
Moreover, the C5+ with its superior light-gathering power has much brighter images than the smaller refractors, and there are plenty of things you can see through the C5+ that don't appear in the refractors.
Incidentally, if you can't see these craters, it doesn't necessarily mean that your optics are at fault. It could be that the seeing just isn't sufficiently good to make them out. It could also be that your secondary is out of collimation. With the secondary essentially acting as a 5x Barlow mirror, the image quality is frighteningly sensitive to proper collimation. I've gotten incredibly picky about the collimation of my C5+, but it returns great dividends, and I find that I encounter a lot more nights "with good seeing" than I do if I don't bother to collimate. (Here are some collimation instructions for the C5+.)
A more extensive treatment of the relationship between obstructions, contrast, and spatial frequency—that is, the breadth of features—can be found on Thierry Legault's page at http://perso.club-internet.fr/legault/obstruction.html.
Copyright (c) 1998, 2006 Brian Tung